Summer-winter notes
17 Sep 2019Some notes for summer 2019, or actually winter 2019, as I moved to Chile.

A picture for the Summer 2019. The Andes.
Queue number again, and applications
A recent result about the so-called queue number was mentioned on this blog in March (see here). The result says that this graph parameter is bounded on planar graph that have bounded degree. The result has now been generalized to any planar graph! The paper is on arxiv and will be presented at FOCS 2019. I haven’t looked into the paper, but I know from David Epptein’s blog that it is a byproduct of showing that “every planar graph is a subgraph of a strong product of a path graph and a bounded-treewidth graph”.
Another recent paper on the arxiv uses this result to design shorter labeling schemes for planar graphs. As the abstract says: “In graph-theoretical terms, this implies an explicit construction of a graph on $n^{4/3}+o(1)$ vertices that contains all planar graphs on n vertices as induced subgraphs”. (Thanks to Cyril Gavoille for pointing out this paper.)
Unfolding polytopes: Durer’s Conjecture
Given a polyhedra, one can cut along the edges to unfold it on the plane as in the following drawing.
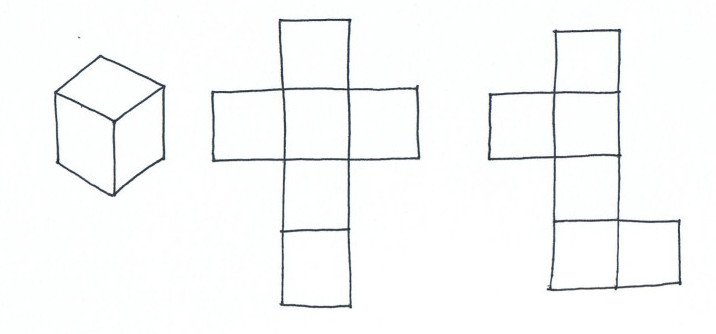
But sometimes, if you cut along some edges, you may have an overlap in the unfolding, as the second unfolding of the following example (borrowed from here) shows.
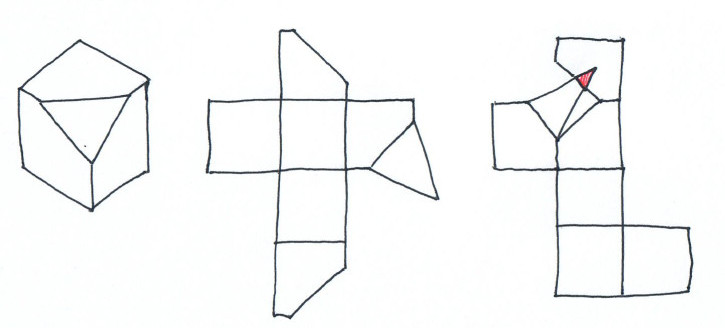
Durer’s conjecture states that “Every convex polytope has a non-overlapping edge unfolding”. A non-overlapping edge unfolding is called a net, so the conjecture can be reformulated as: “Every convex polytope has a net”. It is surprising that such a cute and simple result is still open.
I learned about this conjecture in Eppstein’s report on CCCG. More information can be found in Ten Problems in Geometry by Moritz W. Schmitt and Günter M. Ziegler.
More on graphs inspired by objects and nature
We had a post in april on graphs that have some meaning in terms of real-world objects.
Two additional pointers on this topic:
- a blog post about graph that have one degree of freedom when you want to move them.
- the slides of a talk about graphs inspired by nature, for example by crystals and by bubbles.

The red circles are the nodes on the right drawing, but on the left ones they are part of the procedure to draw the crystals. See the slides for more details.
Automata size to separate two words
Yet another very simple and still open problem: consider two strings of length $n$, what is the size of the smallest deterministic automaton than accepts one and rejects the other? Or more precisely, what is the maximum over all such pairs of this size? The upper bound is polynomial in $n$ (something like $\sqrt(n)$) and the lower bound is $\Omega(\log n)$. An exponential gap!
For more on this see these two posts by Lipton: here and there.
Other notes
- The paper about the matching lower bound that I mentioned here several times won the best paper award at FOCS! I think it’s a remarkable research story: identifying a fundamental problem, telling everybody about it, learning more and more, and finally solving it, and getting an award for it!
- Some day, I’ll learn about spanners, I hope. Here is a recent survey that may help.
- A paper appeared on the arxiv on the recognition of intersection graphs of objects touching a diagonal line, related to this paper of mine.