Discrete notes    About    Archive

STOC and SOCG picks

13 Mar 2019

A few weeks ago the accepted papers lists of STOC and SOCG were made public. A bunch of titles caught my attention, and here are a few bits of information on some papers I could find online.

Testing graphs in vertex-distribution-free models

Graph property testing basically consists in deciding if a graph has a property or not, by looking only at some parts of it. More precisely one queries a few nodes, and ask for their neighbors for example, and then outputs whether the graph has the property or is far from having it. Note that such a statement can only be true with some probability. An introduction to graph property testing is here.

In the classic model, one is allowed to query a random node, with “random” meaning “uniformly at random”. In a new paper the author considers the case where the random access is not uniform but depends on an arbitrary distribution. This in turn implies a change in the definition of being far from a property.

I didn’t dive in the paper, but I imagine the following scenario. Some nodes are more “important” than others. This translates into two things:

For example, you have a dynamic graph, you may not know about newly arrived nodes, but these are less important, so it’s no big deal if you don’t query them now.

[The paper is Testing Graphs in Vertex-Distribution-Free Models, by Oded Goldreich, and will appear at STOC 2019. It was listed in October 2018 property testing review.]

Transportation problem

The transportation problem is the following. Given a graph, where each node $v$ is given a (positive or negative) supply $\mu(v)$, such that $\sum_v \mu(v)=0$, one has to find a flow to transport the supplies in order to reach the configuration where every node has supply 0. See the picture below.

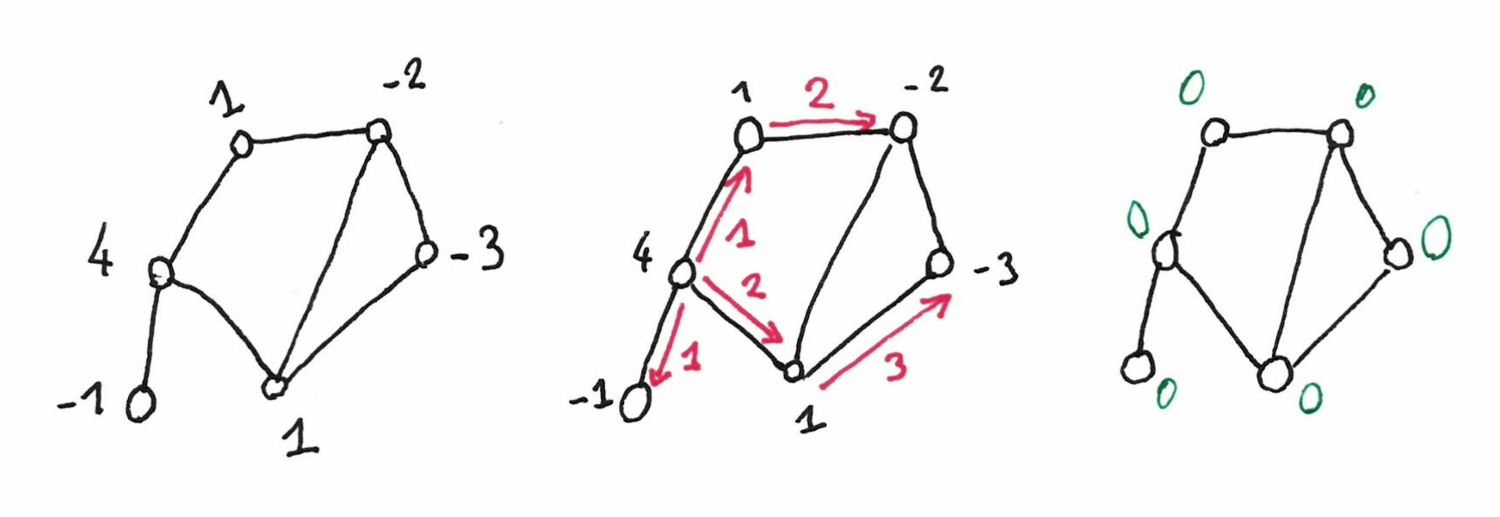
This is very similar to the optimal transport problem in non-discrete mathematics. The paper presents an approximation algorithm for fixed dimensions via continuous optimization.

I don’t know how much continuous optimization is used, but it reminds me of an excellent invited talk by Aleksander Mądry at HALG 2016, that convinced me that continuous optimization can be a good approach to solve combinatorial problems. There is no video of the talk, but this one seems pretty close.

[The paper is Preconditioning for the Geometric Transportation Problem by Boris A. Khesin, Aleksandar Nikolov, and Dmitry Paramonov, and will appear at SOCG.]

LP roundings: iterated meets randomized

A classic approach in combinatorial optimization is to express the problem as a linear program. Unfortunately, only the fractional case is known to be solvable efficiently, and only the integer solutions can be transfered back to solution for the original problem. A solution is to compute a fractional solution and then to round it to an integer solution. This approach is very powerful for approximation algorithms.

There are two important types of rounding: randomized rounding and iterated rounding. In randomized rounding, a fractional variable $x_i$ is simply rounded to 1 with probability $x_i$. In iterated rounding, one iteratively modify the fractional solution until it gets to an integral solutions (for example adding some small amount to a set of variables, until they reach 1, etc.). Both roundings have their pros and cons.

The paper presents a method that combines the two approaches into one common framework, and shows how to use it.

[The paper is On a generalization of iterated and randomizedrounding by Nikhil Bansal, and will appear at STOC.]

Queue layout

Given a graph, a $k$-queue layout is an ordering of the vertices and a partition of the edges into $k$ sets, such that there are not two edges of the same partition, that are nested. Below is an example of a graph and a 2-queue layout of it.

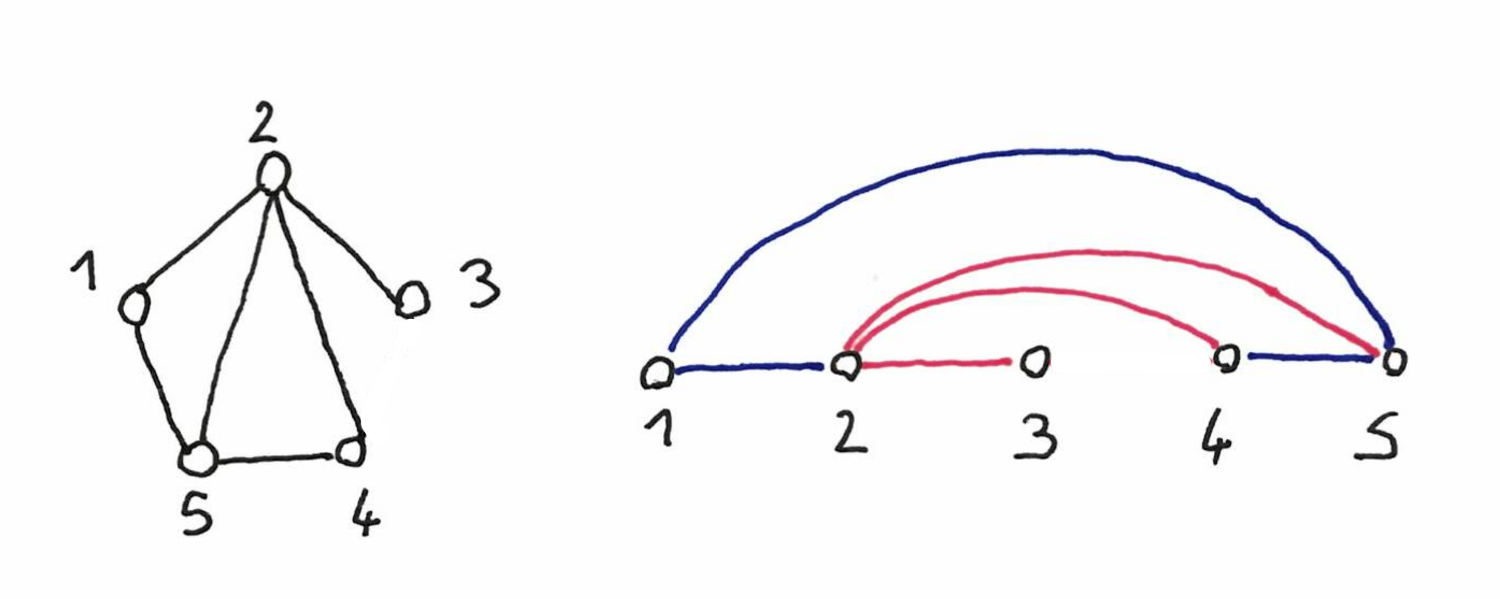
The queue number of a graph is the minimum $k$ such that there exists a $k$ layout of the graph. An important open question is whether planar graph have bounded queue number. The paper makes a step towards a positive answer, by proving that planar graphs with bounded degree have bounded queue number.

[The paper is Planar Graphs of Bounded Degree have Constant Queue Number by Michael A. Bekos, Henry Förster, Martin Gronemann, Tamara Mchedlidze, Fabrizio Montecchiani, Chrysanthi Raftopoulou, and Torsten Ueckerdt. It will appear at STOC (even though the topic is very SOCG-friendly). I didn’t know about queue layouts, and it’s good to discover it, as it is yet another example of graph parameter that correspond to a pattern, in the sense of this paper.]

Reachability of Petri nets

Petri nets are very common in theoretical computer science, for example in model checking. Nevertheless, it is horribly hard to decide the reachability problem for this model: can you get from a configuration $A$ to a configuration $B$? The decidability of the problem was proved only in the 80s, and the best upper bound is non-primitive recursive cubic-Ackermannian (don’t ask what it means, exponential space is already scaring me).

The paper proves that the problem is non-elemetary, that is, its time complexity cannot be bounded by a power tower.

[The paper is The Reachability Problem for Petri Nets is Not Elementary by Wojciech Czerwiński, Sławomir Lasota, Ranko Lazić, Jérôme Leroux and Filip Mazowiecki; and will appear at STOC. In France, Sylvain Schmitz is one of the researcher working on this kind of stratospherical complexities. Simon Halfon one his PhD students at the time, gave an excellent talk on this topic at the IRIF PhD seminar in 2017.]

Quartet distance and 4-cycles

The quartet distance is a distance between phylogenetic trees. More precisely it is a distance between two unrooted trees with labeled leaves. It basically takes all the tuples of four leaves and count how many of them are in different topology in the two trees.

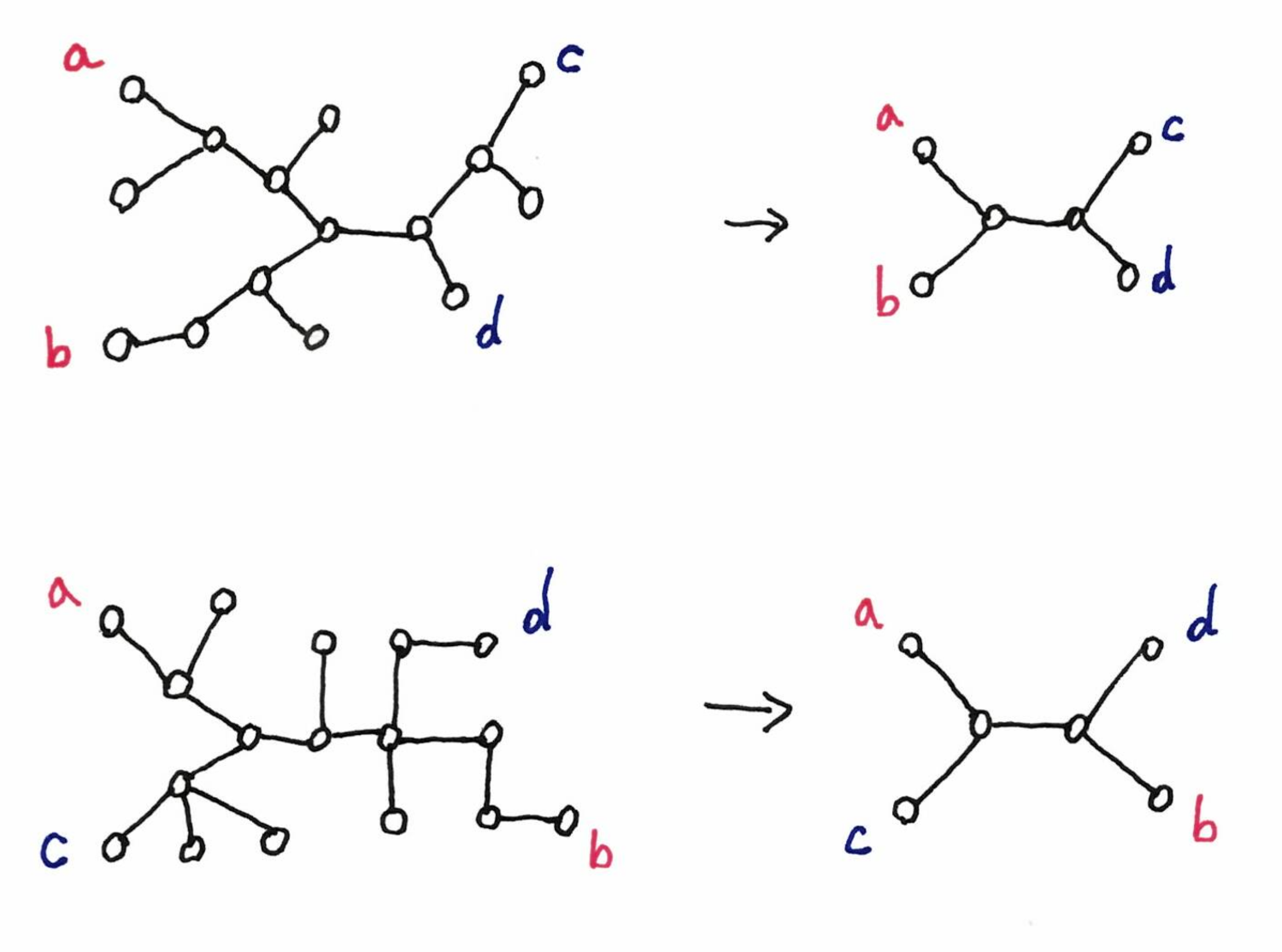
For example in the picture below, for the two trees on the left, we want to decide whether the leaves $a$, $b$, $c$ and $d$ are in the same topology or not. We simplify the tree until we have only these leaves, and we see on the pictures on the right
that it is not the case. Thus this quartet will add one to the distance. (Note that on the left, all leaves should be labeled, but I indicate only the ones we are interested in).

The paper shows that computing the problem of computing distance between two trees is equivalent to the problem of computing the number of 4-cycles in a graph, up to polylogarithmic factors. This implies better algorithms and better insights on the complexity.

[The paper is Computing Quartet Distance is Equivalent to Counting 4-Cycles by Bartłomiej Dudek (whom I have had the chance to meet in EPFL), and Paweł Gawrychowski, and it will appear at STOC.]

© 2024. All rights reserved.