Simulation argument IV. Maximal matching

15 Feb 2019

This is the fourth and last post of a series about the simulation argument, that started with this post.

In this post we tackle the maximal matching problem. Or actually we will show why establishing a lower bound for this problem is not as easy as for the sinkless orientation problem. The real lower bound is in this paper.

Encoding

A maximal matching is a set of edges of the graph, such that no two of these edges are adjacent, and no two unmatched node are linked by an edge.

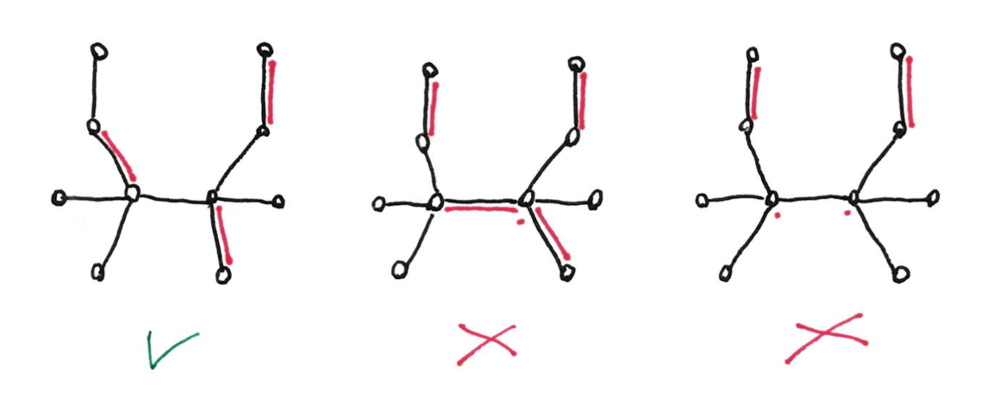
A natural encoding for this problem would be to label the edges of the matching with a label $A$, and edges not in the matching with a label $B$. But this does not work for our setting. Instead, we will do the following. (As in the previous post we will deal with 2-colored trees.)

The edges of the matching are labeled with the label $M$.
If a white node is not matched then its edges are labeled with $P$. These are pointers to matched black nodes.
The remaining edges are labeled with $O$.

On the following picture, red edges are for $M$, green edges are for $P$, and blue edges are for $O$ (the missing edge should be blue!).

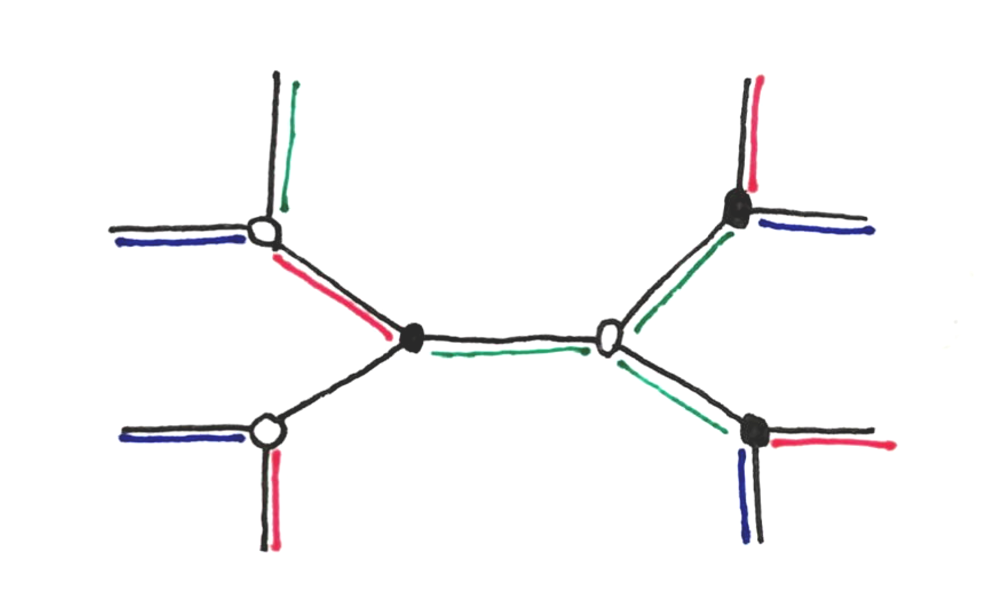
The languages we use are then described by the following polynomials:

$L_W = MO^{\Delta-1}+P^{\Delta}$,
$L_B = M(P+O)^{\Delta-1} + O^{\Delta}$.

Transformation

Simulation

We perform the simulation on a black node $u$, and get a polynomial $P_u$.
By definition $P_u\subseteq (M+O+P)^{\Delta}$, and is factorized.

Product property

As the product rule applies, we know that $P_u \subseteq M(P+0)^{\Delta-1}+O^{\Delta}$.
Thus there is at most one factor of $P_u$ with an $M$.

Claim 1: This factor is either $(M)$ or $(M+O)$.

Proof: Suppose the factor with $M$ has a $P$. Then it means that when we develop $P_u$, there are two monomials $M\times K$ and $P\times K$, with $K$ a polynomial of degree $\Delta-1$, that does not contain an $M$. But the monomial $P\times K$ is not included in $M(P+0)^{\Delta-1}+O^{\Delta}$. which contradicts the product property.

Then we are left with 5 possible sums as factors in $P_u$: $(M), (O), (P), (M+O), (P+0)$.

Now it seems that we cannot get much more out of our properties, so let’s try a simplification step.

(Tentative) Simplification step

If we can map $(M+O)$ and $(P+O)$ to a simple label, and still match the language, then we are done, and we can conclude like in the previous post. But this is not going to happen.

Suppose you are in following situation, which is supposed to be easy because there is not even a $(P+O)$. (On the picture, every black node writes on its adjacent edges.)

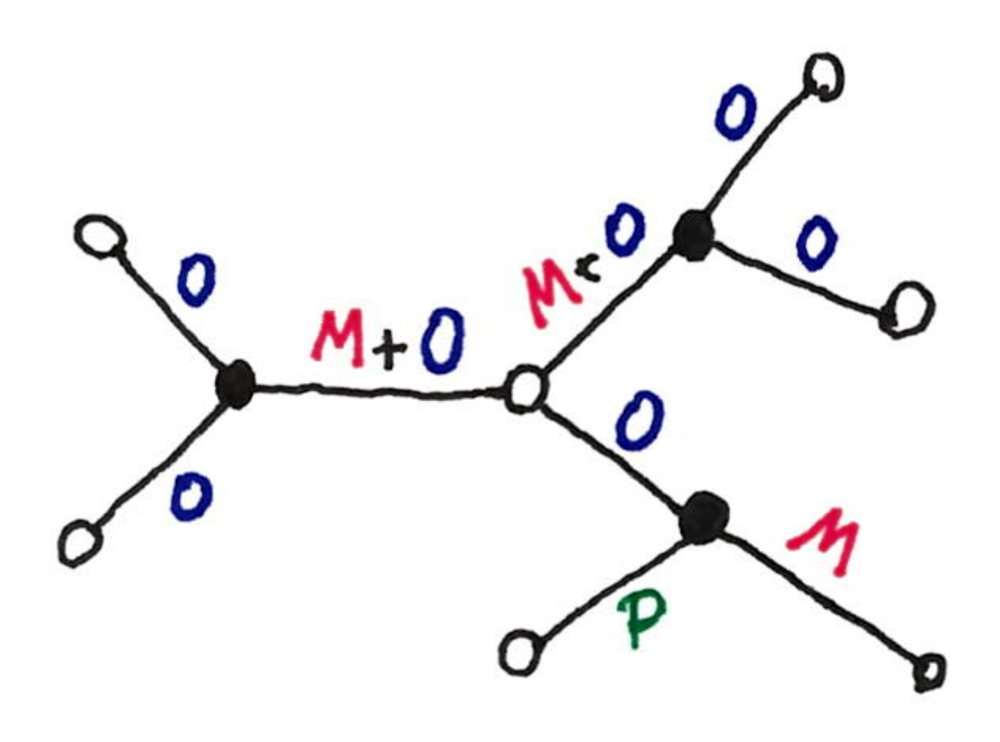
Ok, let’s just take one of the two edges labeled with $M+O$ (let say the one with the smallest port-number on the white node), label it with $M$, label the other one with $O$, and we are done.

This does notwork. The problem is the one we highlighted in the second post: the edges are not uniformly set-labeled by all the nodes. A concrete bad case:

let $(u,v)$ and $(v,w)$ be the two edges labeled by $(M+0)$
in its simulation, $u$ has (M+O) for both edges, and based on port-numbers, decides that $(u,v)$ gets $M$.
in its simulation $w$ has $(M+O)$ for $(v,w)$, but only $(O)$ for $(u,v)$. Thus it labels $(v,w)$ with $M$.

To solve this problem you have to synchronize, and this is forbidden as it takes extra time.

No lower bound this way

So at the end, we cannot conclude like in the case of sinkless orientation.

Comments on that:

This makes sense: actually there is a $O(\Delta)$ algorithm for this problem, thus no $\Omega(\log n)$ lower bound exists.
The above alone does not prove that there is no $\Omega(\log n)$ lower bound: we could use another definition of the problem, or we could have tried more exotic label replacement ($M$ transformed into $P$, or whatever).
If you want to prove a $\Omega(\Delta)$ lower bound then you need to be smarter. In particular you need that, after the transformation, the language is different. Basically there should be a parameter that starts with something like $\Delta$ and decreases at each transformation. For that, see the paper!

Thanks to Mikaêl Rabie for reading and improving this series of posts!