Simulation argument III. Sinkless orientation

13 Feb 2019

This is the third post of a series that starts here.

---

---

In this post, we show how to use the simulation argument to prove a lower bound on the sinkless orientation problem. This is done in the context of the previous post, that is, 2-colored $\Delta$-regular trees.

Sinkless orientation encoding

The sinkless orientation problem consists in orienting the edges of the graph, such that no node is a sink, that is, no node has only edges pointing to it.

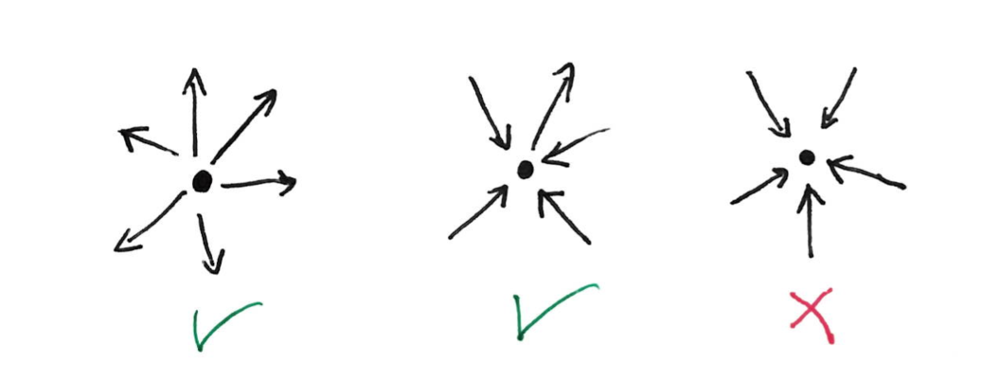
In a bipartite graph, whose nodes are labeled black and white, it is easy to encode an orientation with edge labels: an edge is labeled $b$ if it is pointing to the black endpoint, and $w$ if it is pointing to the white endpoint.

Now the languages, described as polynomials, are:

• $L_W=b(b+w)^{\Delta-1}$,
• $L_B=w(b+w)^{\Delta-1}$.

Because white nodes must have an adjacent edge pointing to a black node, and vice-versa.

Transformation

We will show a very strong property: from a $T$-round algorithm for sinkless orientation, we can get a $(T-1)$-round algorithm for… the exact same problem of sinkless orientation!

Simulation

After one step of simulation centered at a black node $u$, the labeling of the edges adjacent to $u$ is described by a factorized polynomial $P_u$. By definition $P_u$ is included in $(w+b)^{\Delta}$.

Product and consistency property

We now use the key properties to have a better upper bound on $P_u$. Thanks to the product property, we know that $P_u\subseteq w(b+w)^{\Delta-1}$. Now consider a white node $v$, and the set labels given by its black neighbours. Because of the consistency property, there must at least one of its edges labeled with $b$, that is $P_v$ cannot be $w^{\Delta}$. And well, that’s all we need!

Simplification step

Consider the simplification: $b+w \rightarrow b$.

If we apply this simplification, we have all the edges labeled with unique labels (not set labels), and this labeling is correct with respect to the black language. In other words, after simplification, we have a polynomial $\hat{P_u}$, that is a monomial, and $\hat{P_u}\subseteq L_B$.¹ But what about the white nodes? We know from the previous section that $P_v$ was not $w^{\Delta}$, thus $\hat{P_v}$ is not $w^{\Delta}$ either, thus $\hat{P_v}\subseteq L_W$.

Thus we have a new labeling, for the exact same language, in one less round!

Lower bound

The same reasoning would work if we center the analysis on the white nodes. This means that from any $T$-round algorithm for sinkless orientation, we get down to a 0-round algorithm for sinkless orientation. And sinkless orientation is not a trivial language.

So is sinkless orientation impossible to solve?

No, remember that our lower bound technique works only up to $O(\log n)$ rounds. Thus we have just proved an $\Omega(\log n)$ lower bound for this problem.

Actually there is a $O(\log n)$ algorithm for this language, hence this bound is tight.

Footnotes