Notes from pre-COVID19 times

01 Apr 2020

Hi there! After abruptly coming back to France because of the virus, I resume blogging (instead of traveling, basically). Here is a set of notes that I wrote before the quarantine and everything.

A picture from the pre-COVID times.

Shapley value

The Shapley value is a concept in game theory. It basically describes how a group of players that have played collaboratively, should share the pay-off of the game, taking into account that some players have contributed more than others. In other words, it is a way to measure how important is each player for the team. For some settings it is proved to be the optimal way to share the gain, with respect to some objective of fairness.

The setting is the following. There are $N$ players, $1,2, …, N$, and a function $f$ from the subsets of players to the set of possible pay-offs (eg $R$). For a subset $S$ of players, $f(S)$ is the pay-off that the players of $S$ would get as a whole if they were to collaborate together.

Now, assume that all players collaborate, and get some pay-off $P$. How should we distribute $P$, using $f$? The idea is the following. First chose an arbitrary order on the players, for simplicity, let say the natural order $1, 2, …,N$. Then player $1$, gets $f(${$1$}$)$, player $2$ gets $f(${$1,2$}$) - f(${$1$}$)$ etc. That seems pretty reasonable: every player gets the marginal value it adds to the pay-off. Now this is not always fair, because of the ordering that we chose arbitrarily. Therefore one normalizes this by taking the average over all permutations of the individual pay-offs. This is the Shapley value.

[Thanks to Eric Remila for telling me about this.]

Stochastic dominance

Stochastic dominance is a concept of probability that is useful in (algorithmic) game theoretical settings, such as secretary-type problems.

Let $A$ and $B$ be two real random variables. Then $A$ stochastically dominates $B$ if for every $x$, $P(A\geq x)\geq P(B\geq x)$, and for some x, the inequality is strict. In terms of cumulative distribution function, this means $F_A(x)\leq F_B(x)$ for all $x$, and with strict inequality for some $x$.

This notion is useful in the randomized online setting: you want to show that your online algorithm obtains, in expectation, at least half the payoff of a “prophet” that would play knowing all the game in advance. Then it is sometimes useful to show that your algorithm stochastically dominates “half the prophet”.

[I heard about this by working in the group of José Correa in Santiago de Chile.]

Polygonization, a problem not known to be easy or hard

There are not so many reasonable problems for which we have neither a polynomial-time algorithm nor a proof of NP-hardness. Some well-known are graph isomorphism and integer factorization. Wikipedia has a list in its NP-intermediate article. Here is a counting problem that falls into this category.

A polygonization of a set of points is a simple polygon that visits all the points. In the following picture, the points are black and a polygonization is drawn in blue.

The algorithmic problem is: given the point set, count the number of polygonizations it has.

See the two posts by Eppstein on special aspects of this problem, here and there.

Liquid rope coiling and discrete model

When you pour some honey on a pancake, you can see that the honey behaves a bit like a rope and can get some rotational movement when touching the pancake. Something like this:

[See also this video by Jearl Walker.]

Something strange about this is that there is no reaon a priori for the movement to be rotational: it’s just something (the honey) falling on something else (the pancake). I was curious whether this could appear in a very simple discrete model. I started thinking about a sandpile model (like the one mentioned here recently) to simulate the behaviour of the honey, but at the end I tried to design the most simple model that would “create rotation”. Here is a naive model, that does not have a sandpile flavour (and probably makes little sense), but shows some rotation, without explicitely refering to a rotation.

Start with an hexagonal grid representing the pancake (because it’s easier than a square grid). The yellow cell is where the honey is currently arriving, and the orange circle is the projection of the origin of the honey (e.g. the spoon) on the pancake.

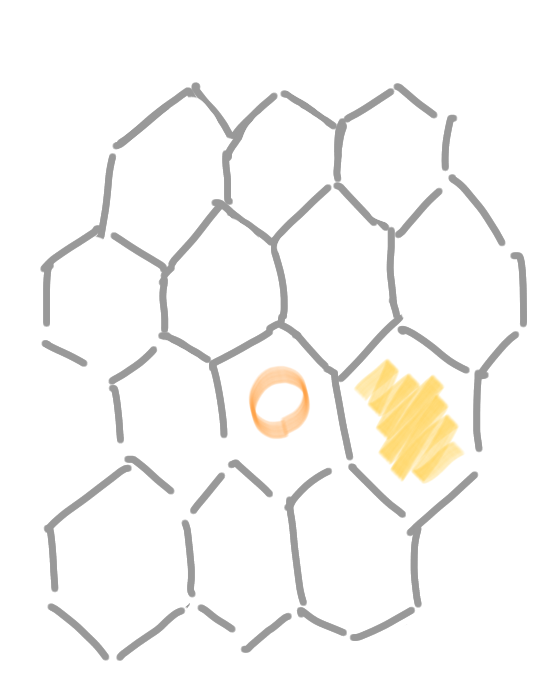
Now there are two forces. One is the “speed” of the yellow patch, that simulates the fact that the honey tends to go where there is less honey, and the very last cell visited has more, so is repulsive. It is represented by the yellow arrow. The other one is the attraction of the orange circle, that simulates the fact that the honey is still “tied” to the spoon. It is represented by an orange arrow. Now the average of the two forces is the red arrow, that is pointing to the next cell.

The proccess is repeated, and the yellow patch is circulating around the cell with a orange circle.

Well it’s not a very fancy model, in particular it doesn’t make a difference between honey on a pancake, and a planet around the sun, but maybe it can be improved..!

Anyway, physicists prefer continuous models, and a paper about the modelization of liquid rope coiling is available here.

[I learned about research on liquid rope coiling in this article in the French popularization magazine “Pour la science”.]

Other notes