March notes I.

25 Mar 2019

First half of the March 2019 notes.

Mimosa in Jardin des Plantes.

Tverberg’s theorem

For geometric algorithms in the plane, one sometimes has go through case by case analysis along the lines of “if this point is below this line, then this and that intersect, if not then…”. Such proofs are a bit boring and it is easy to make mistakes. So when you have a general theorem that does the work for you, it’s good news. Tverberg’s theorem looks like a theorem that could be useful from this point of view.

Tverberg’s theorem states a condition such that the convex hulls of several sets of points intersect. Precisely: in a $d$-dimensional euclidian space, for any integer $r$, for any set of $(d+1)(r-1)+1$ points, there exists a partition in $r$ subsets such that the convex hulls of the $r$ subsets intersect. The picture below present the case $d=2$ and $r=3$, for $(d+1)(r-1)+1=7$ points, and for one less point. In this last case the theorem does not hold (we just show one partition).

[I saw the name of this theorem on the SOCG accepted papers list, unfortunately the paper is not available online, and we don’t know what they do with this theorem.]

Criteria for fair item assignment

Fair item assignement consists, given items and participants, to assign the items to the participants in a fair manner, for some definition of fair. There are many variants of the problem and many ways to define fairness.

Here are a few fairness criteria, to decide if the assignment is fair or not:

Max-min fair-share (“I cut, you choose”): every participant is least as happy as if she had cut the set of items first, and then let all the other participants choose before her.
Max-min fair-share (“You cut, I choose”): the same but reversed, that is every participant is at least as happy as if someone else did the cut, and she could decide first.
Envy-freeness: no participant would like to change her items for the items of another participant.
Competitive equilibrium from equal incomes: there exists a price for each item such that, given the same budget, the participants would choose different items.

[I learnt about this at the CS PhD seminar of Sorbonne university, by Parham Shams.]

Tai chi problem

When crossing the Jardin des plantes I often witness the following kind of scene.

It is people practising taichi. There is a professor in front of the group (with a white cap on the picture) who is showing the movements, and everybody is supposed to perform them in real-time (it’s pretty slow).

The thing is: people on the first row can see the professor, but the ones on the back cannot, so they follow the moves of the people on the rows closer to the professor. Therefore there is a kind of wave from the front to the back. Maybe it can make an interesting problem: how fast does the wave propagate, is it close to a straight line, how does it depend on the size of the participants?

Core algorithms deployed

It is common as a reseacher to have doubt about how useful your research is. In my case, I sometimes wonder whether the algorithmic problem we try to solve really have an impact. It could well be the case that the algorithmic problems that are really useful are the ones that have only basic answers. That is, we focus on the sweet spot between trivially easy and trivially hard problems, and this set could have an empty intersection with real-world questions.

I was really happy to discover a few years ago the topic “core algorithms deployed” on stack exchange, that removes any doubt on this regard.

Numerical errors in missile trajectories

I discovered in the introduction of this PhD thesis the following story, illustrating why computer arithmetics is important and difficult.

In 2011, a US “defence missile” missed a “real missile”, with tragic consequences, because of computer arithmetic. The basic reason is the following. There used to be a software doing the trajectory computations, with rounding operations, including on the time variable. This variable slowly shifted compared to the real time because of these rounding. It sounds dangerous, but it was actually ok: the trajectory computations would consider fast movements so between the start and end of the trajectory, the shift was negligible, and the absolute time did not matter. The problem is that part of the system was updated with more accurate time variable. Then the shift would not be the same in two different parts of the system. Then the shift would not cancel out and this was the bug.

[A better explanation can be found in this document. The PhD thesis has a more light-hearted story about gamers trying to finish a video game level without jumping, and using a slow shift of a platform (also due to rounding errors) to do so.]

Max cut and planar graphs

Two results about max-cut that I didn’t know:

a cut is maximum if and only if its complement is a minimum odd-circuit cover (this is easy to check, see for example here, or simply stare a bit at the picture below.)
This can be used to obtain a polynomial-time algorithm for max-cut in planar graphs.

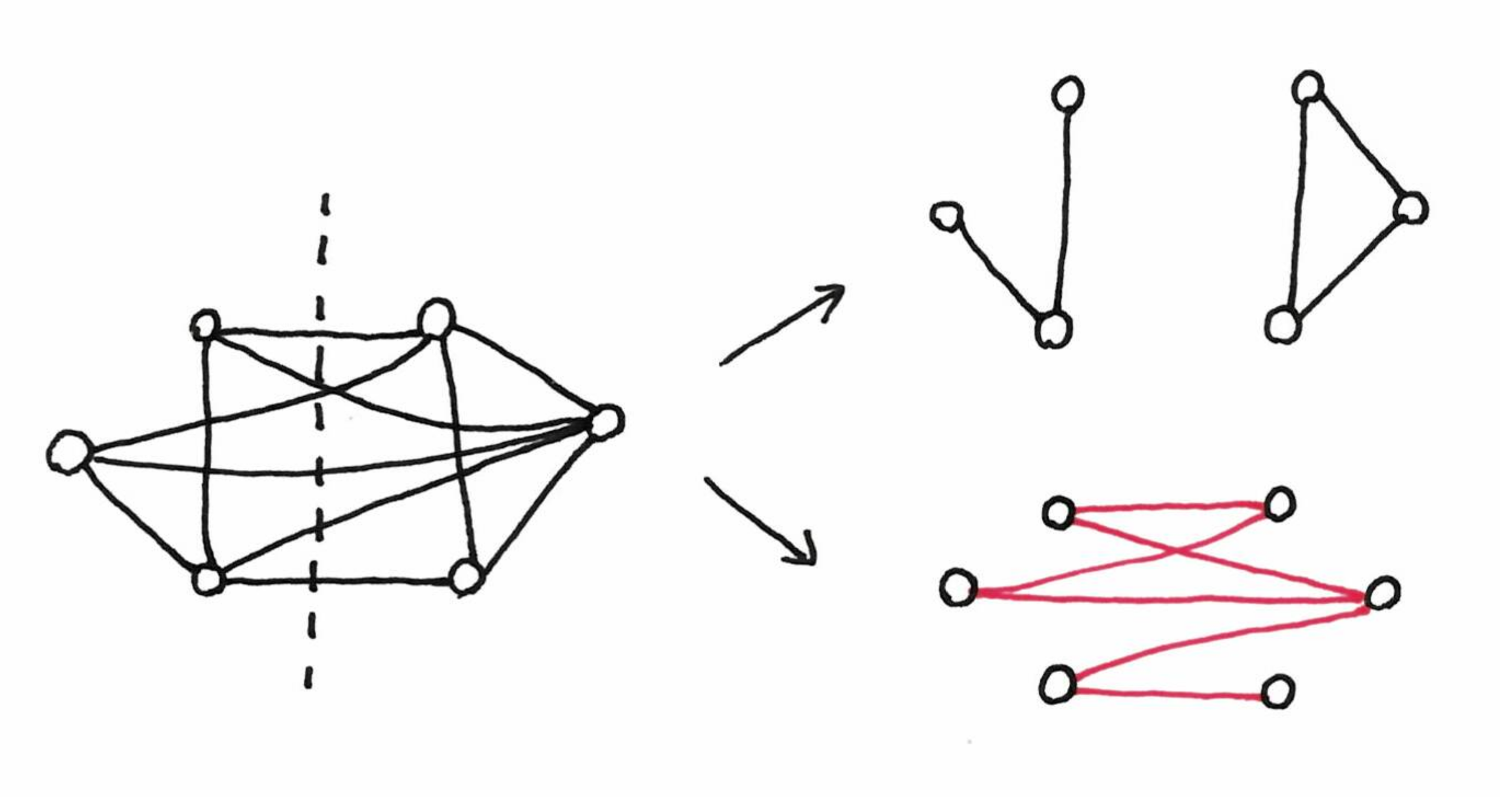
[I got aware of this by this preprint which presents an algorithm for max-cut whose complexity is parametrized by the number of crossing in the drawing of the graph.]

Discrete notes About Archive