Discrete notes    About    Archive

October 2019 notes: distances and moving stuff

07 Nov 2019

Some notes for October 2019, related to distances and to moving stuff.

A lot is going on in Chile in October 2019. Fortunately there are some good recipes.

Matching graphs via Gromov-Hausdorff distance

There are many contexts where one would like to compare two graphs, to measure if they are close or not. One way of doing this is to decide whether one is included in the other (the subgraph isomorphism problem) or more generally if they have a large isomorphic subgraph. Another way is to measure the number of edits one has to make to go from one graph to the other (for example the number of edges to add and remove). This is what is done in property testing, where having a distance on the objects is essential.

More generally, there exists a distance for compact metric spaces called Gromov-Hausdorff distance, that applies to graphs.

No surprise, this distance is a complicated notion (an inf of a max of a sup of an inf), and computing it is NP-hard. The reduction is to the quadratic bottleneck assignment problem, a facility location problem.

A fairly recent preprint studies how to estimate a modification of this distance in polynomial time.

Hardness of moving earth

Given two point sets of equal size in an Euclidian space, $A$ and $B$, and a bijection $f: A \rightarrow B$ , the cost of transporting $A$ to $B$ through $f$ is the sum over the elements of $a$ of the distances from $a$ to $f(a)$.

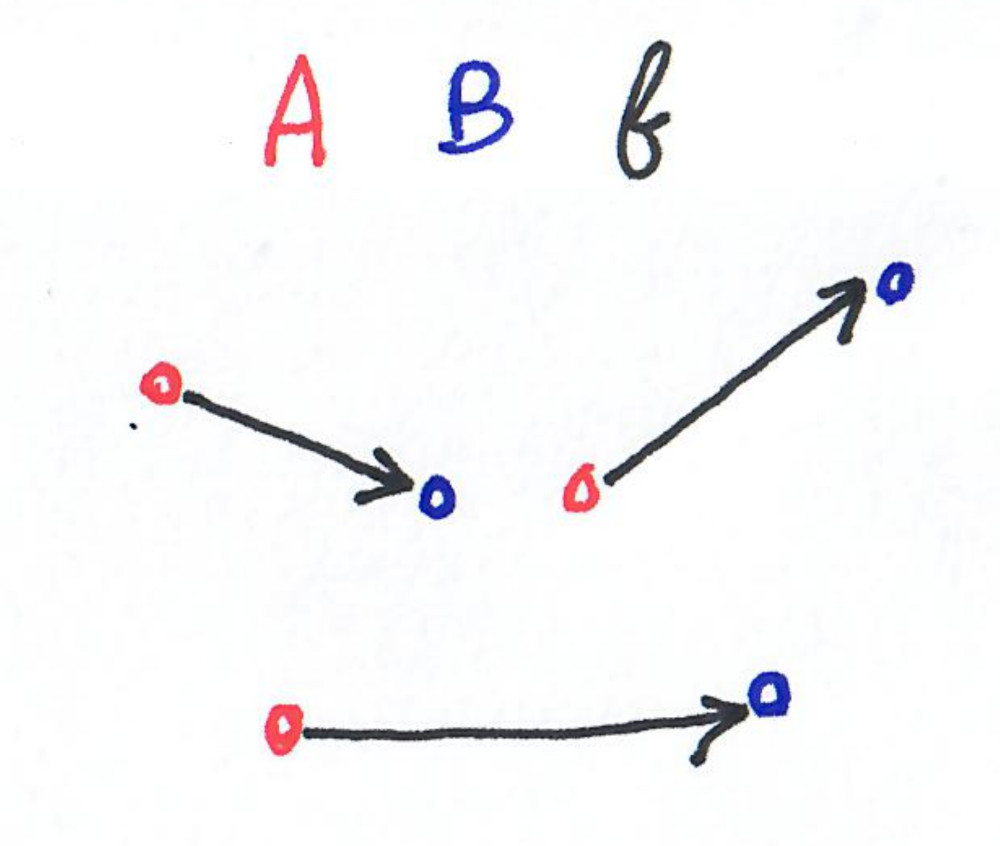
Now given two point sets, the earth mover distance is the minimum such distance over all bijection: $ EMD(A,B)=\min_f \sum_{a\in A} d(a,f(a)) $

It is the discrete analogue of Monge-Kantorovich metric in probability theory, and is used in machine learning.

Algorithms to compute the EMD are quadratic in $n$, and faster algorithms are known for approximation but only in small dimensions.

A recent preprint proves conditional hardness results that explain this situation.

Complexity of sandpiles

Sandpile models are models close to cellular automata, based on a grid in some dimension $d$, where every cell has a number (the number of grains of sand there is at this location), and there is a local rule to decide where the grains move at each step.

There is a recent survey about the complexity of predicting the final shape of sandpiles. There are some very nice things going on. For example the complexity of the prediction is related to the computational power of the sandpile itself:

A classic sandpile model is called the abelian sandpile model (or Bak–Tang–Wiesenfeld model) and is the following. On a grid $Z^d$, the rule is: every node that has $2d$ grains or more gives one grain to each neighboring cell.

Here is an example with $d=1$, and a starting configuration where one cell has 5 grains. The cells that have 2 or more grains are “unstable” and give one grain to their left neighbor and one grain to their right neighbor.

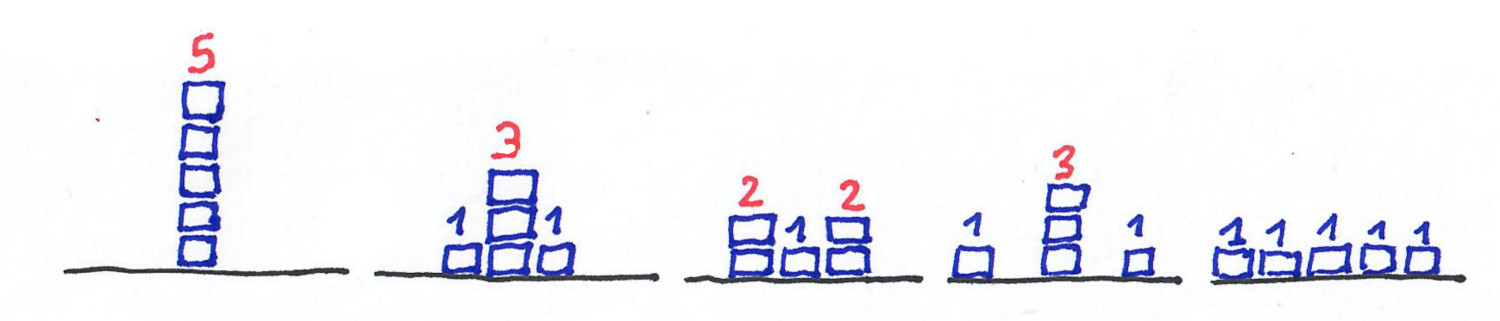
Note that the dynamic is not exactly what you would expect from a real sandpile, but it is very simple and has very nice properties.

For this model, the following hold:

The survey gives a lot results, sketches and conjectures.

k-OPT ratio for TSP

2-OPT and its generalization k-OPT, are popular heuristics for the (metric) traveling salesman problem. They consist in iteratively looking for 2 (respectively $k$ edges) to modify to improve the cost of the tour. Here is an example for 2-OPT.

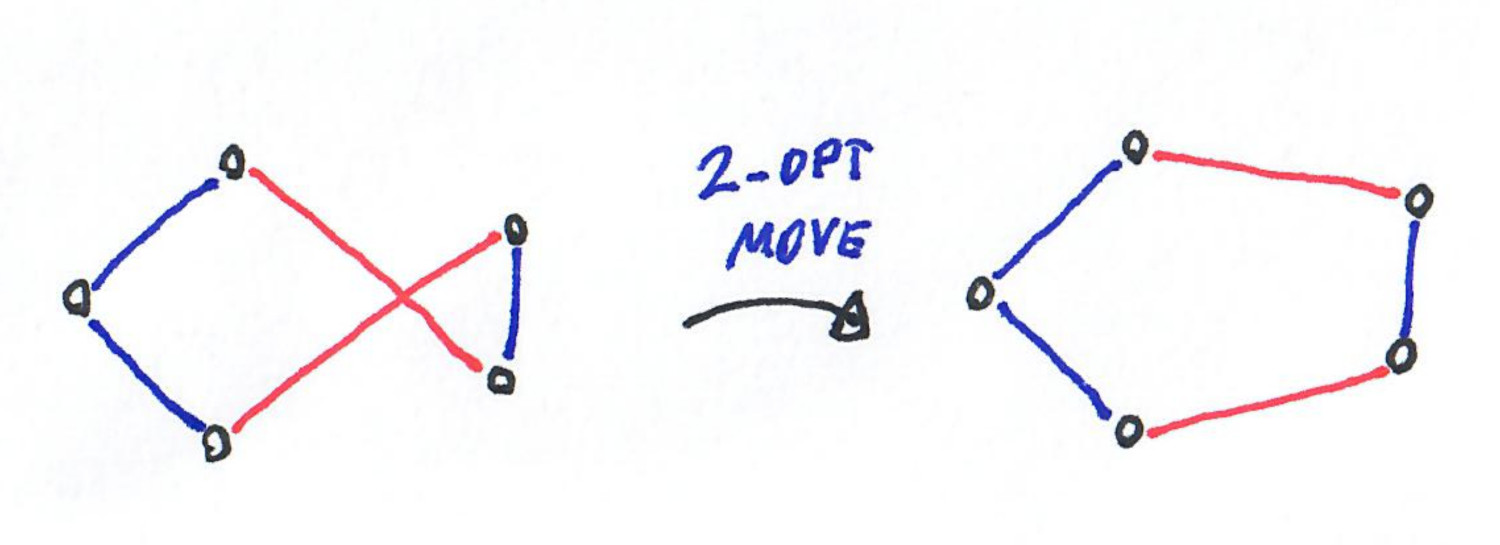
This heuristic performs poorly in the worst-case: exponential time, and approximation ratio in $\theta(\sqrt n)$. But it performs well in practice.

A recent preprint computes the precise approximation ratio for 2-OPT, which is $\sqrt(n)/2$.

Other papers from the literature prove that :

© 2024. All rights reserved.