Impossibility proof techniques: from distributed to online
12 Mar 2022Last year, I wrote a teaser about our SODA paper The secretary problem with independent sampling (joint work with José Correa, Andres Cristi, Tim Oosterwijk, and Alexandros Tsigonias-Dimitriadis). Today, I’d like show how we could transfer a bunch of ideas from distributed computing to online computing to prove impossibility results. This is not a complete proof, but an overview of the techniques.
The problem
The problem is an extension of the classic secretary problem:
- An adversary chooses a set of $n$ numbers and orders them.
- Then, for each number independently: with probability $p$, it joins the sample set ; and with probability $(1-p)$, it joins the online set.
- The player is given $n$ and the sample set.
- The numbers of the online set are presented one by one to the player, in the order chosen by the adversary.
- The player wins, if and only if, she stops on the maximum of the online set.
See the teaser post for the origin of this problem, and the other variant, where the order is random and not adversarial.
Context
Quite early in our study of the problem, we realized that a simple threshold algorithm (the most common type of algorithm for secretary-like problems) seemed optimal. Unfortunately, the classic approach in this area to prove optimality, which consists in proving that one can restrict attention to a specific set of algorithms, would not work with the sampling extension.
We proved that the algorithm was indeed optimal, following a completely different paths: we showed an upper bound on the optimal performance, and that bound happened to match the performance of the threshold algorithm.
I will now list a few ideas of this upper proof.
Playing with parameters
A classic assumption in secretary-type problems is that the player knows the length $n$ of the sequence. This can be questionned, since in real life one might not know this length, but it prevents silly counter-examples, e.g. when there is only one number.
To make our life easier, we tried to remove the assumption that the player knows $n$, and checked what would happen. Note that since we have the sampling set (and know the sampling probability $p$), we still have some estimate of $n$.
This idea of playing with the assumptions regarding the knowledge of the parameters is common in distributed computing, where one might assume (or not) that the nodes know the size of the network, the maximum degree, etc.
Also, we assume for now that $p=1/2$, and that the algorithm must be deterministic.
More structured instances and reduction
A second idea that is common in the distributed computing community is to consider the easiest (and maybe quite artificial) problem we cannot solve, solve it, and then generalize little by little. Here the idea was to make the simplifying assumption, that the adversary does not chose the ordering of the numbers: they are presented in increasing order. If the player knew the length of the sequence, then this would be trivial, since the maximum is the last value. But without this knowledge, it’s not so easy.
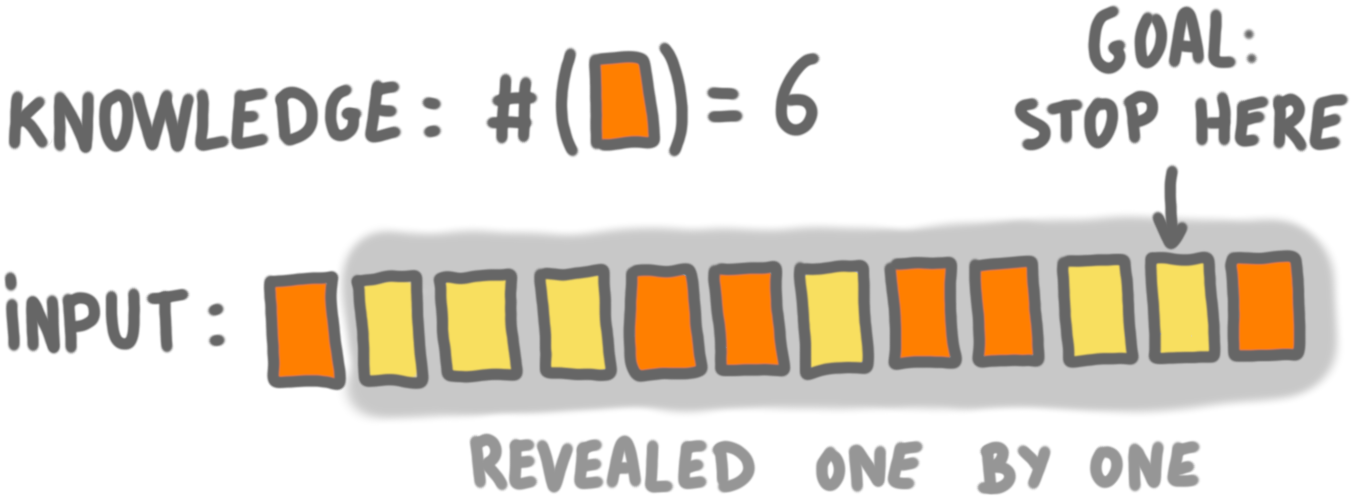
The problem becomes equivalent to what I call the “Last yellow card game”:
- There are $n$ cards, where $n$ is unknown to the player.
- There is a deck of $n$ cards, and each of them is yellow with probability 0.5 or orange with probability 0.5.
- The player is given the total number of orange cards.
- The cards are revealed one by one, and the player should stop on the last yellow card.
Identifiying indistinguishability situations
As mentioned in the previous post, indistinguishabilty is a classic technique in distributed computing. It consists in finding two situations in which the algorithm should make different decisions to be correct, but cannot, because it has the same view of the system. Here is how we can adapt this technique to our setting.
Consider two instances of the game:
- Instance 1: the sequence of cards is yellow, yellow, orange.
- Instance 2: the sequence of cards is yellow, orange.
At the beginning of game the player cannot distinguish between these instances: she does not know the length, and for both instances, she knows that there is one orange card in the sequence, and that the first card is yellow. Then, either in this situation she decides to stop, in which case she wins in Instance 2, but looses in Instance 1, or she decides to continue and then looses in Instance 2, and maybe wins in Instance 1 (if she stop on the second yellow card).
In other words, these instances are in conflict: no algorithm can win in both.
Building a conflict graph
One of the classic results in distributed graph algorithms is the $\Omega(\log^*n)$ lower bound of Linial for coloring. The proof of Linial consists in building a meta-graph, where every vertex represents a neighborhood at some distance $d$ in the original graph, and then to study this graph. We use the same type of idea.
We build an infinite graph, where the vertices are all the possible instances (that is, all the sequences of orange and yellow). The edges represent the conflicts between the instances. For example, on the picture below, we can see an edge between yellow-orange and yellow-yellow-orange. (The picture does not show all the edges of the graph, only the ones between instances of consecutive size.)
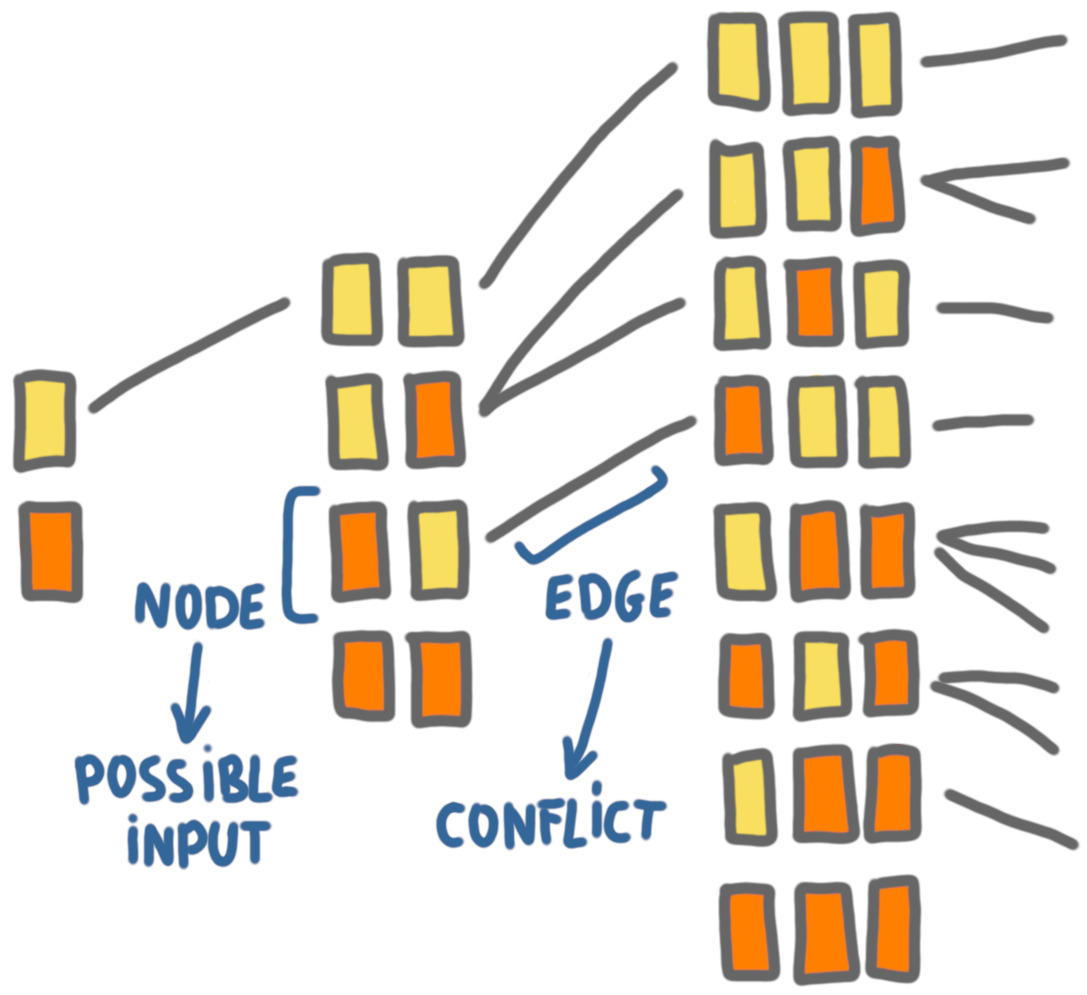
Now, the key property is that for any algorithm $A$, the instances where $A$ succeeds form an independent of the graph, because of the indistinguishability argument.
We study the structure of the graph (which takes a few pages), and prove upper bounds on the size of such independent sets, which translates directly into upper bounds on the performance of any algorithm. (The performance is measured as the minimum on $n$ of the probability of winning on instances of size $n$, which is why it is meaningful to consider the instances ordered by size.)
Generalizing
Now that we have the result for the modified problem, with unknown length and increasing order, we have to go back to the original setting. We do this by considering that the adversary chooses some secret time $k$, and put numbers in increasing order until $k$, and then chooses only low numbers like the picture below. It is easy to see that this simulates the previous case.

Removing the assumption that the algorithm is deterministic and that $p=1/2$, only requires a more intricate analysis of the conflict graph.