Teaser: The secretary problem with independent sampling

30 Jun 2021

I recentely presented the paper The secretary problem with independent sampling at the Highlight of algorithms conference in the three-minute format (+ poster). Here is a blog version of this teaser talk.

The paper is joint work with José Correa, Andres Cristi, Tim Oosterwijk, and Alexandros Tsigonias-Dimitriadis.

The secretary problem

The secretary problem is a classic problem of online algorithmics. Basically, some numbers are presented to a player, one after the other, and the player has to stop on the largest number.

More precisely, an adversary chooses a set of $n$ numbers, these numbers are presented to the player in a random order, and for every number, the player has to decide either to discard it, or to keep it. The decisions are irrevocable: if a number is discarded then it is destroyed, and if a number is chosen then the game is stopped, and this number is the output of the player.

The player wins if and only if the number she chooses is the maximum number.

Of course this is very hard, and one cannot win all the time. But surprisingly there is an algorithm that is guaranteed to pick the maximum with probability $1/e$. (See the wikipedia article linked above.)

At this point, we have discarded a 2 (the turtle) and a 1 (the rabbit), and we see a 5 (the cow). We know that there are $n=4$ numbers (animals) in total. So maybe, it's a good idea to stop there.

Issues and our new model

A problem with the secretary problem, when it comes to modeling real-world situations, is that it is very pessimistic: we start with absolutely no knowledge about the numbers. The fact that we can still ensure $1/e$ is because the order is random, and if we had an adversarial order, then we couldn’t guarantee anything.

In the adversarial order, anything can happen.

In general, in a real-life situation (say in auctions), one has some idea about what the numbers (that is, the offers) will be. This can be modeled with replacing the adversarial inputs by inputs generated by a distribution, but this approach also has issues (e.g. how do you know the exact distribution?).

We propose a new model summarized in the following picture.

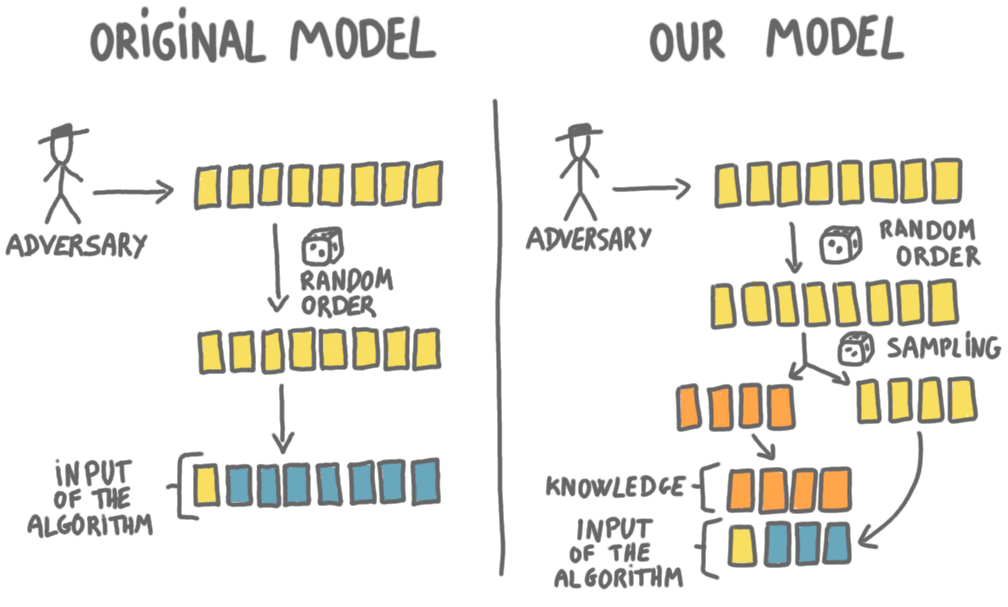
The classic and the new secretary model.

The left column represents the classic secretary model. In our model (the right column), the beginning is the same: an adversary chooses $n$ numbers, and these numbers are shuffled at random. But then there is a twist. Each number will join a “sample set” with probability $p$, and will stay in the “online set” with probability $(1-p)$. In the picture, the orange cards are the sampled numbers, and the yellow cards are the ones that stay in the online set. The numbers in the sample set are removed from the game, they are given directly to the player at the very beginning. The player sees these numbers, and then plays only on the online set. In other words, the sample set is a way for the algorithm to learn about the way the adversary chooses the numbers. (In some sense, the sample set is a training set, and the online set is a test set.)

The rational behind this model is that the samples model the past data that we know about when we start the game. Still having an adversary makes the model more robust than having a distribution, and samples are closer to the type of knowledge one would have in real-world scenarios.

Results

In our new model, we can consider both the classic random order and the adversarial order for the numbers arrivals. For these two variants we give algorithms with optimal success guarantee. Unsurprisingly, in both cases the larger the sampling probability $p$ the better the guarantee. (See the paper for the curves.)

The proofs of optimality in the two cases are very different: in the first case we make the problem more continuous and use tools from optimization, whereas in the second case we introduce a new technique for proving impossibility results, based on indistinguishability arguments similar to the ones used in distributed computing.