A research story about patterns in graphs (2)
15 Sep 2020This is the second post of a series about the story of a paper on patterns and graph classes. The first post is here.
After discovering that our class of diagonal rectangle graphs had been studied by other people in our own university, we discovered that we were not only two groups chasing this class.
Second twist, segments and parabolas
José Soto came back from a postdoc in Germany at some point of my stay in Chile. We told him about our problem and solution and he told us he had just attended a Master defense in Berlin where the same class was studied. The student was Thomas Hixon, and his advisor Stefan Felsner. They ended up with this class following yet another path.
They were studying segment graphs, which are just intersection graphs of segments. These are quite popular graphs ; in particular Scheinerman’s conjecture (now a theorem) states that every planar graph can be represented as the intersection of segments.
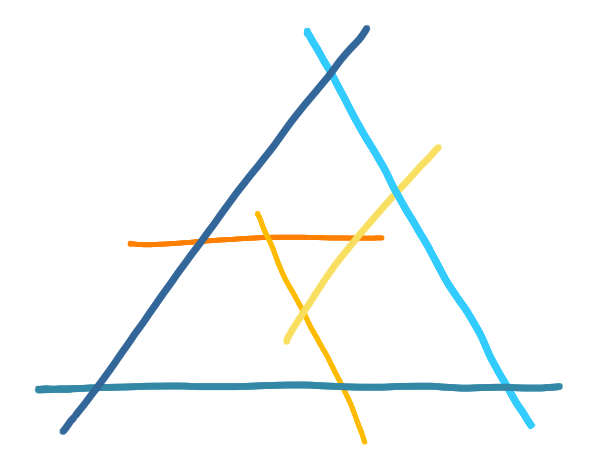 |
 |
When studying such graphs a popular way to look at special cases is to allow only some directions for the segments. For example, on the drawing above all segments have angle $0$, $\pi/3$ or $2\pi/3$ with the horizontal. But Hixon and Felsner went into another direction, which is to allow only segments lying on the set of lines tangent to a parabola.

It happens that this defines intersection graphs that have the same characterization as our class, thus is actually the same class. And even worse for us, they had the same kind of algorithm for maximum independent set… Actually, José Soto even knew about an older paper by Lubiw which had an algorithm for the same class of graphs. She had arrived to this class by generalizing interval graphs (in the same kind of perspective as Mauricio and Christopher from the previous post).
I was quite depressed to discover that I had worked all this weeks in vain, and José (Correa) told me something like: “It’s actually good news: if people have already answered our questions, it means that we have good questions and that’s the most important part.” (At the time I was not completely convinced that this was good news!)
In the end, we could strengthen our results in various ways (more general rectangle configurations, faster algorithm, results about integrality gap etc.), and it became my first paper.
Meanwhile, I had been playing with the kind of characterization we had, with forbidden configurations and an ordering, which is the main topic of this series. More in the next posts.
Epilogue about diagonal rectangle graphs
Believe it or not, yet another group had been “discovering” the same graph class at the same period. This we learned from Hixon’s thesis, which was citing it.
Cantanzaro, Chaplick, Halldórson, Halldórson and Stacho, had introduced max point-tolerance graphs, as a variation of tolerance graphs. They defined it as a model for biology. More precisely, they too had the point of view of intervals with points, and these represented segments of DNA with a special position, for example a suspected deletion.
Cantanzaro et al. and Hixon et al. ended up merging the papers. It’s a bit crazy how four completely independent groups studied the same graph class at the same moment (+ it had been studied before).
Years later I presented some results about graphs at GROW 2017 and mentioned this class without naming any authors or the story, and at the end of the talk Steven Chaplick (one of the authors of the merged paper) came to me and told me “by the way this class you mentioned, it is known, it is not new”: he was afraid I might be re-re-re-re-re-inventing it!