Contraction sequences
19 Nov 2021Contraction sequences is a new point of view on some graph algorithms concepts such as Courcelle’s theorem. It arises from the study of a new parameter called twinwidth. The paper developing the concept will appear at SODA next year, and is on the arxiv here. Edouard Bonnet gave a talk on the topic at our local graph meeting two weeks ago, and this week a longer one at the French Graph and Algorithms days. Here are some notes on the topic, following the structure of the introduction of Edouard’s talk. We can find the slides of the long talk here.
Warm-up with cographs
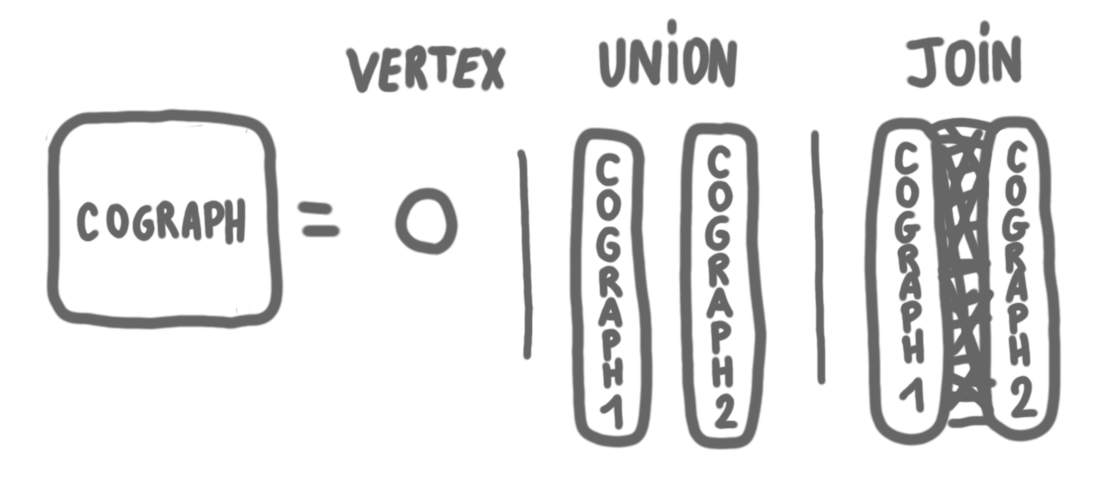
Let us start with a warm-up. We will consider a specific graph class, and a simple independent set algorithm for this class. The cographs are the graphs that can be built iteratively in the following way:
- A single vertex is a cograph.
- The union of two cographs is a cograph.
- The join of two cographs is a cograph (where a join is taking the union of two graphs, plus all the edges between a vertex in the first graph and a vertex in the second graph.)
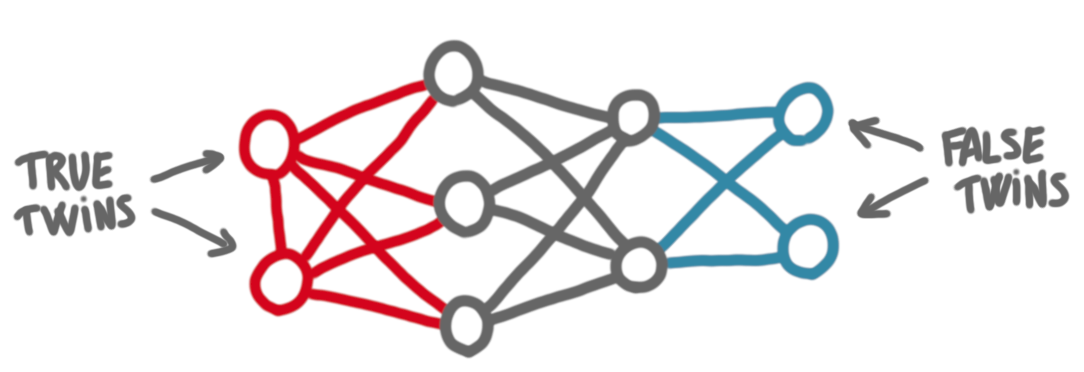
Cographs have the following property (which is actually a characterization). In a cograph, every induced subgraph has at least two vertices with the same neighborhood. These are called twins. More precisely, true twins are twins that are adjacent one to the other, and false twins are twins that are not adjacent.
Let’s design an efficient algorithm for maximum independent set using this property. We will maintain a partition of the vertices, and at first every vertex is in its own part of the partition. In other words, there is a bag for each vertex. We will maintain a maximum independent set in each bag. At the beginning, every vertex is the maximum independent set of it own bag.
Now, let’s take two twins of the graph. We will merge their bags. If the twins are false twins, then the solution is the union of the two vertices. If the twins are true twins, then they are linked by an edge, thus we cannot take both in the solution. We chose arbitrarily one of the two vertice to stay in the solution. For the rest of the algorithm, we will consider that we have merged these vertices into one. We will call this operation a contraction. As the twins have the same neighborhood, it is easy to define the adjacency of the new vertex: it is again the same neighborhood.
Note that after the merge, we have an induced subgraph of the original graph, hence the twin property still holds. We iterate the contraction operation, but now in a more general context, where the twins are bags with more than one vertex. Let us note that each time we make a contraction we preserve the following properties:
- If two bags $A$ and $B$ are linked by an edge in the contracted graph, then every couple $(a,b) \in A\times B$ corresponds to an edge in the original (uncontracted) graph.
- If two bags $A$ and $B$ are not linked by an edge in the contracted graph, then no couple $(a,b) \in A\times B$ corresponds to an edge in the original graph.
If we have false twins, we simply take the union of the solutions from the two bags to create the solution for the merged bag. If we have true twins, we cannot take vertices in both bags, because of the complete bipartite graph between the two bags. We take the solution of the bag that has the largest solution, and erase the solution from the other bag.
Let’s take an example. At first, every vertex is in its part of the partition.
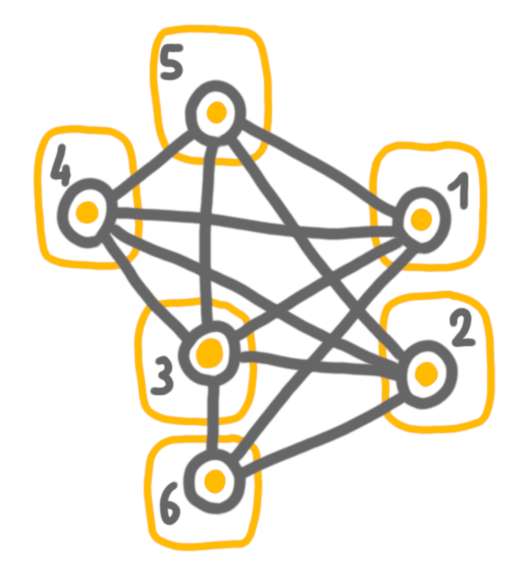
Then we contract 1 and 2, which are false twins. And then 4 and 5, which are true twins. In the first case, we keep both vertices in the solution. In the second case, we have to chose, and we keep 4 (arbitrarily).
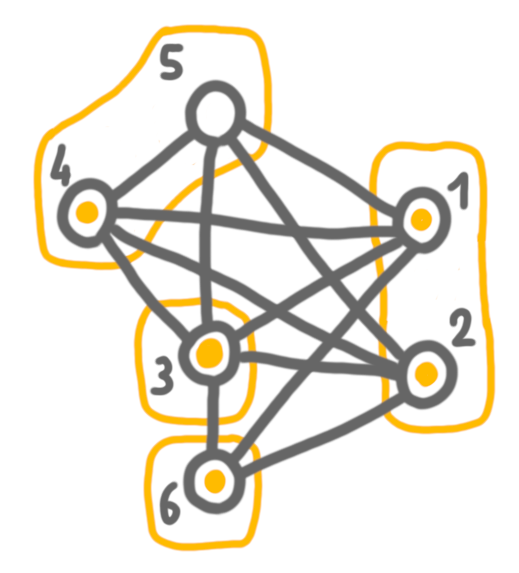
Next, we merge 4+5 with 6, which are false twin bags, and keep both solutions.
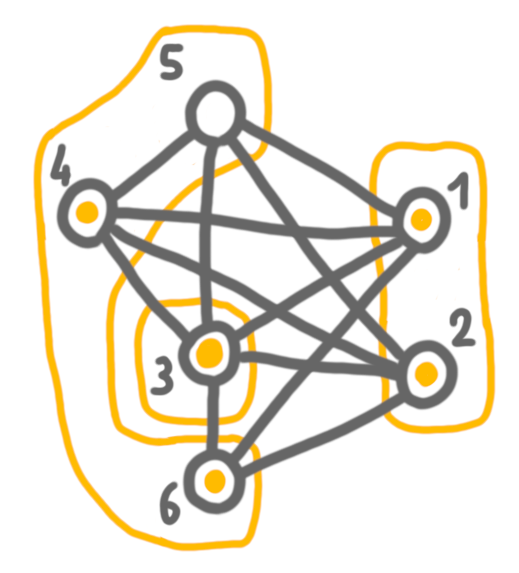
Then 3 and 4+5+6, which are true twins, and here we chose to keep the solution of 4+5+6, because it is larger.
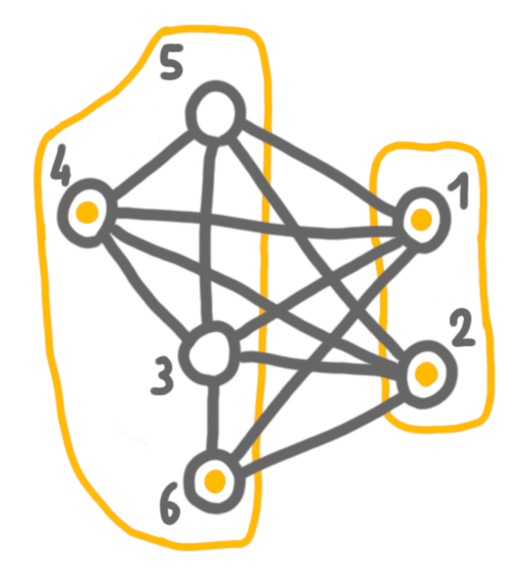
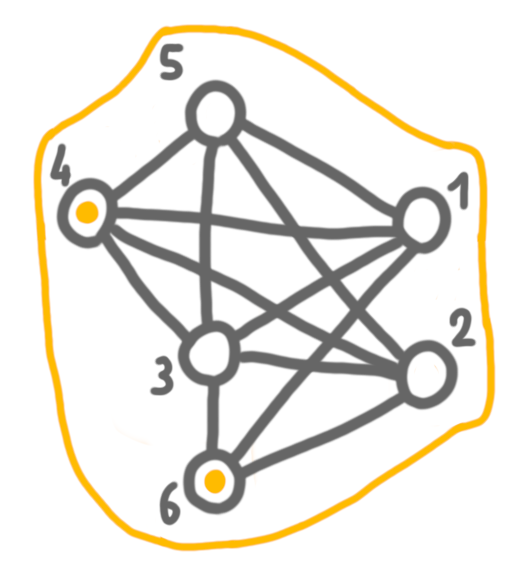
Finally, we merge 4+5+6 with 1+2, and keep the solution of the left side. The outcome is a maximum independent set.
Contractions for general graphs
Cographs have this very nice structure that two bags are either linked by nothing or by a complete bipartite graph. In general graphs, it is not possible to define a contraction sequence with such strong constraints. The general notion of contraction sequence uses three types of edges between bags: edges, that correspond to complete bipartite graphs, non-edges, which correspond to “no edge”, and red edges which correspond to cases where there are some edges, but not all of them. At a given step of the sequence, the red graph is the graph of the red edges. Below is an example of a contracted graphs, with some red edges, and what the partition looks like on the original graph.
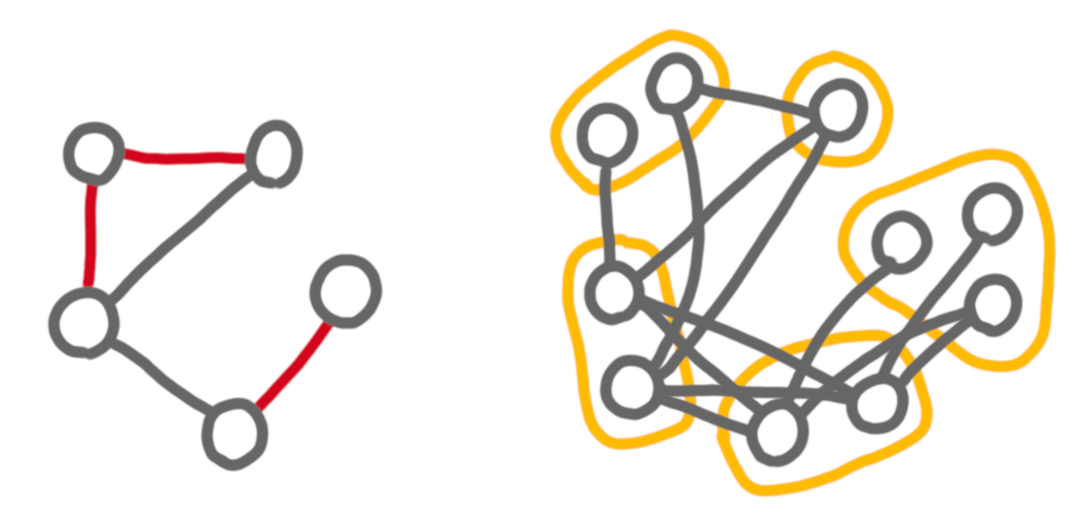
A cograph is then a graph that admits a (general) contraction sequence with no red edge. More generally by putting constraints on the successive red graphs given by the sequence, we can redefine several interesting notions.
For example, consider the maximum degree of the red graph in the sequence. The minimum such value (over all sequences) is equal to the twinwidth of the graph. Other examples are the size of red components, which is related to rankwidth, and the number of red edges, which is related to the linear rankwidth.
Algorithmic consequences
Contraction sequences is a good framework to design algorithms: one “just” has to prove that taking one step of the sequence does not take too much time. Very very roughly if the size/size-of-connnected-component/degree of the red graph is small, then it means that for many contractions, things are easy, like for cographs. When there are red edges, then we might need to do complicated things. It is fairly natural to expect FPT-flavored results parameterized by a measure of the red edges.
Contraction sequences can be used to get a new proof of Courcelle’s theorem. Remember that Courcelle’s theorem basically says that any problem that can be described by a logical formula of some type (a graph MSO formula), of length $l$, can be solved in time $O(f(l,t).n)$, in a graph of treewidth $t$ and size $n$, where $f$ is an arbitrary function. The idea of the proof is that one can maintain at each step which formulas are true in each bag, just like we kept a correct independent set in the case of cographs.