Diameter lower bound in local certification (3)
16 Apr 2021This is the third post about the certification lower bound of diameter. The first post is here. In this post I will describe the precise reduction construction that works in the framework that we have seen in the second post.
The content of this post is again based on Approximate Proof-Labeling Schemes by Keren Censor-Hillel, Ami Paz, and Mor Perry.
What we are looking for
We want to define two transformations $x \mapsto H_1(x)$ and $y \mapsto H_2(y)$ that we will put together to form a graph $G(x,y)$ of the following form.

Let $t$ be the size of $x$ and $y$. We want two properties:
1 - $DISJ(x,y)=TRUE$ if and only if $DIAM(G(x,y))\leq k$.
2 - The $H_i$ should have $O(\sqrt{t})$ nodes.
The first one ensures that the reduction makes sense, and the second ensures that we get the correct lower bound at the end.
Encoding the bit strings in the edges.
The natural idea to encode of bit string of length $t$ into a graph of $\sqrt{t}$ nodes is to encode each bit into the existence or not of an edge. We are going to do something similar but not exactly that. The reason is that we want to control the diameter, so we want instances that are more structured.
Let’s focus on Alice’s input $x$. First we put the string into a matrix, such that any bit can now be refered to as $x_{ij}$ (resp. $y_{i,j}$).
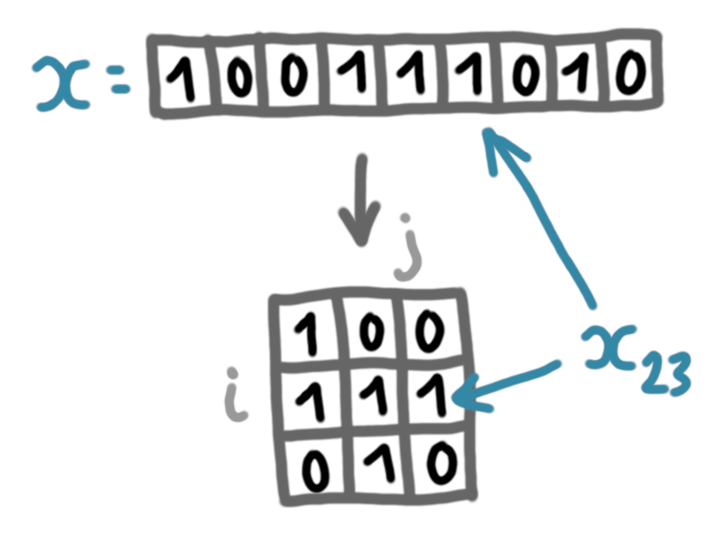
(Let’s assume that $t$ is a square number.)
Now, we define a graph with two sets of nodes, the $a_i$’s and the $b_j$’s.
All the $a_i$’s form a clique and all the $b_j$’s form another clique. There is an edge between $a_i$ and $b_j$ if and only if $x_{ij}=0$. Note that it is the opposite as one would expect (eg in an adjacency matrix).
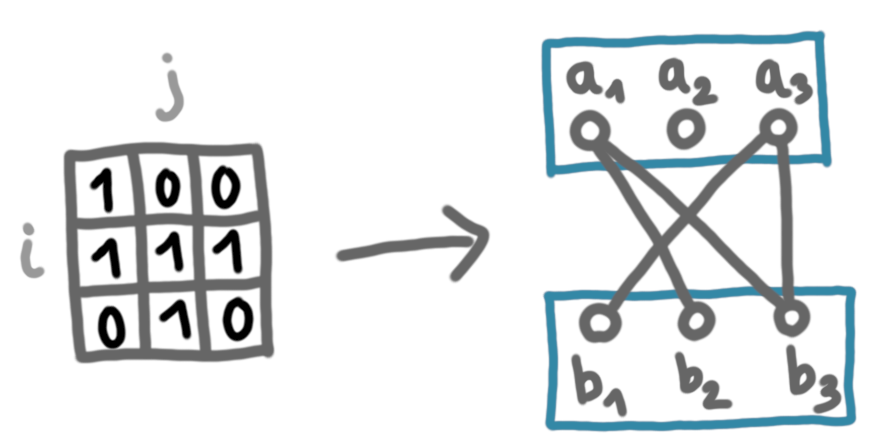
Putting things together
We have shown how to build the gadget of Alice from $x$, and we actually follow the same process for Bob, just naming the nodes differently: the nodes $(c_i)_i$ are the analogues of $(a_i)_i$, and the nodes $(d_j)_j$ are the analogues of the nodes $(b_j)_j$. We add a node $\ell$ that is adjacent to all the nodes $(a_i)_i$ and $(b_j)_j$ and a node $r$ that is adjacent to all nodes of $(c_i)_i$ and $(d_j)_j$.
Then, we add paths of length $k-1$ between the pairs ${a_i,c_i}$, between the pairs ${b_j,d_j}$ and between $\ell$ and $r$.
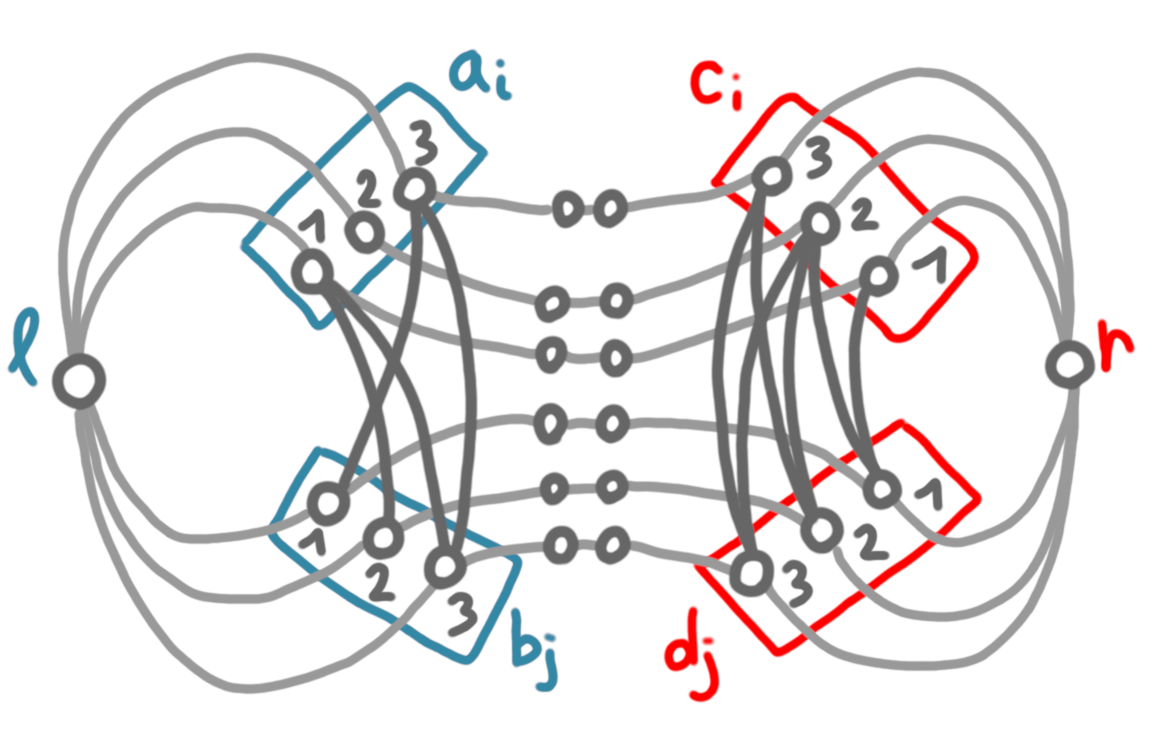
(On the picture, $k=4$ and the paths have length $k-1=3$.)
That’s it that’s the graph. It has $O(\sqrt{t})$ nodes as announced.
Checking the diameter
Now we have to check the first property, $DISJ(x,y)=TRUE$ if and only if $DIAM(G(x,y))\leq k$.
The important part of the argument is about distances between $a_i$’s and $d_j$’s (or similarly the distance between the $b_j$’s and $c_i$’s), so let’s focus on these nodes.
Let’s first assume that $DISJ(x,y)=FALSE$. Then there exists some $i$ and $j$ such that $x_{ij}=y_{ij}=1$. In our construction, this means that neither the nodes $a_i$ and $b_j$ are linked by an edge, nor $c_i$ and $d_j$. Now let’s look at the distance between $a_i$ and $d_j$. The shortest path between $a_i$ and $d_j$ must take one of the paths that go from left to right of length $k-1$. Then if this path has length $k$, it means that it uses just one edge in addition to the left-right path. One can check that this is not possible: the only edges would work are the edges $(a_i,b_j)$ or (c_i,d_j) and these are not part of the graph. Therefore the shortest path between $a_i$ and $d_j$ has length at least $k+1$ and the diameter is at least $k+1$.
For the second implications, let’s assume that $DISJ(x,y)=TRUE$. Then for every couple $(i, j)$, it should be that either $x_{ij}=0$ or $y_{i,j}=0$. Thus at least one of the edges $(a_i,b_j)$ or $(c_i,d_j)$ belongs to the graph. Then for any couple $(a_i,d_j)$, there is a path of length $k$: use the edge $(a_i,b_j)$ or $(c_i,d_j)$ and continue with the relevant (k-1)-paths. Thus here the diameter is $k$ as promised. (In this case, one also has to prove that the there is no other couple of nodes with distance larger than $k$, but this is not very interesting.)
That’s it.