Can we always build and certify at the same time? (MST with fragments)

06 Oct 2020

This is the second post of a series about self-stabilization. (The first post is here). Many self-stabilizing algorithms build and certify a solution at the same time, and the main question of this series is whether this is always possible if one insists on space and time efficiency.

We will discuss this question on a particular problem: minimum spanning tree. To do so we first need to describe the classic structure of MST algorithms, and the certification that follows. That’s what this post is about.

Building an MST with fragments

The classic way to build a minimum spanning tree (MST), is to use so-called fragments. This technique originates from Borůvka’s algorithm and is used in the celebrated GHS algorithm. We will describe this approach on the following weighted graph.

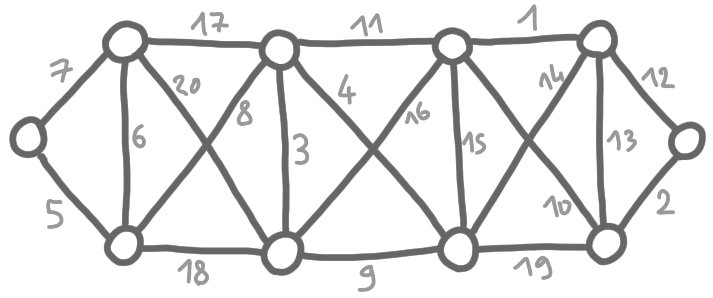
The general method is the following. We will select edges little by little. At any point of the algorithms, there are fragments, which are sets of nodes, such that they are connected by a spanning tree of selected edges. At the beginning, every node is its own fragment. When a new edge is selected, the two fragments of the two endpoints merge, that is, the two sets of nodes merge into one set, and the two spanning trees are connected into one spanning tree. It can be that more than two trees merge at the same time. At the end of the computation there is only one fragment, with one spanning tree, and this spanning tree has minimum weight.

Now let’s get into the details with our example. (For simplicity, we do not rewrite all the weights on all the pictures.)

First, every node chooses the lightest among its adjacent edges. In the picture, a yellow arrow $u \rightarrow v$ means that $u$ chooses $(u,v)$.

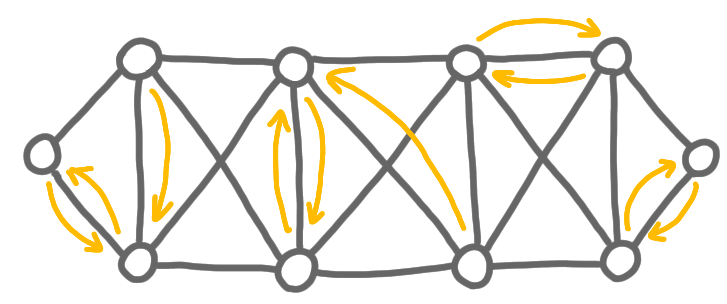
For now, we consider only the case where the edge weights are distinct, like in our example. Then there is no choice for the nodes, and all the edges that have been chosen by at least one node are selected. The set of selected edges forms a forest, and each tree of this forest is a fragment.

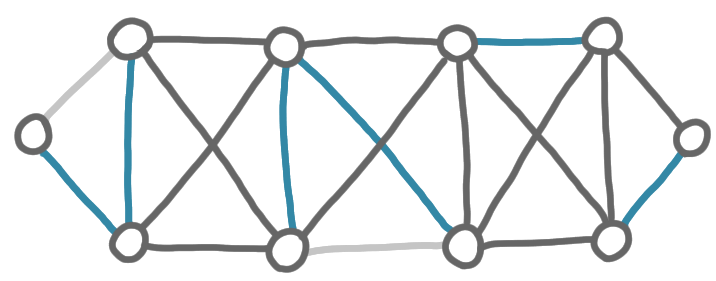
(In the picture above, the non-selected edges between nodes of a fragments are more transparent, because they will not be useful anymore.)

So now for the second phase, every fragment chooses the lightest out-going edge that is the lightest among all edges that have exactly one extremity in the fragment.

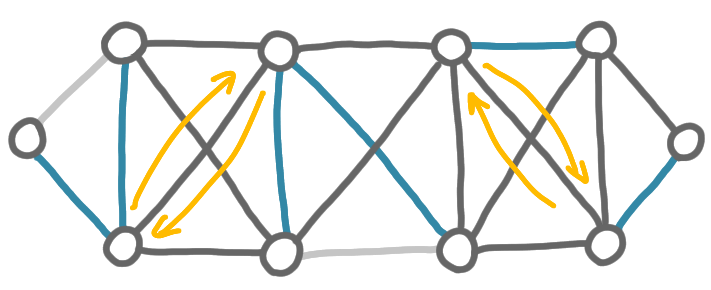
And again, we merge the corresponding fragments by selecting the chosen edges.

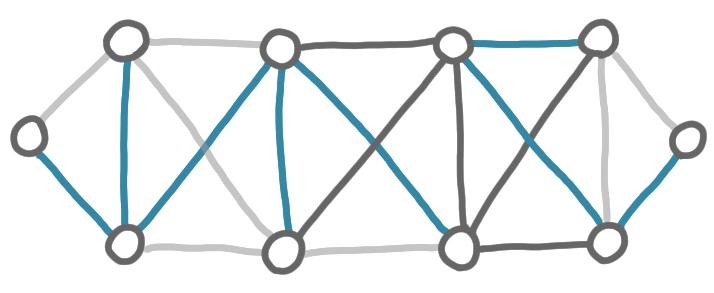
The last phase is the one where the last fragments get merged.

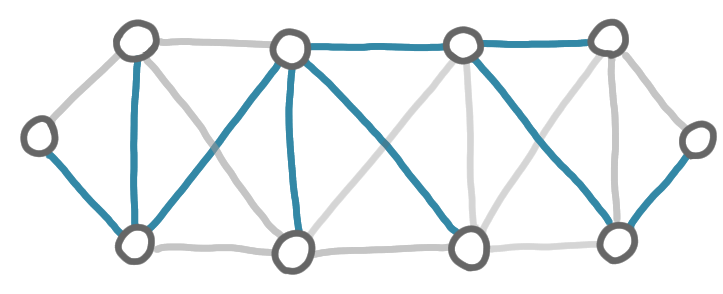
And we get the final tree, which is a minimum spanning tree.

Properties

Here are a few comments about this process. We will reuse some of these properties in the next post.

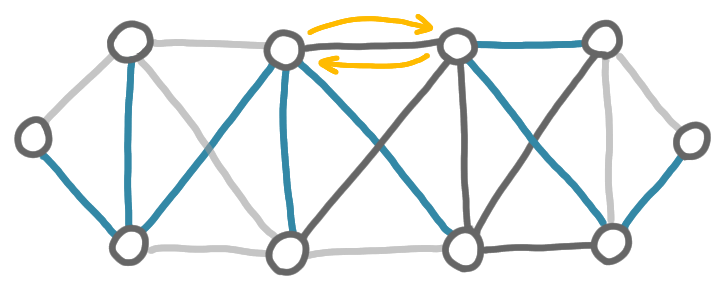
• Here we have assumed that the weights are distinct, but in general this is not the case. If not, then we need an extra step, where the nodes decide which of the lightest outgoing edges will be selected. Also an extra-step is needed in case two fragments choose ceach other to merge, but using different edges. Again the nodes can decide which edge wil be kept.

• The process is incremental: the edges that have been added in an early phase are kept during the whole computation and appear in the final MST.

• There are at most $O(\log n)$ phases, because the number of fragments is at least halved at each phase.

• In the process, the merging is quite uncontrolled: it could be that a fragments merges with just one other fragment (like in the two last phases in the example), but it can also be two (like in the first phase, in the middle and on the left), or actually $\Theta(n)$.

• Also the place where the fragments merge is uncontrolled: a large fragment can be merging with one fragment in some places and with another fragment very far away.

MST certification

It is possible to certify an MST by basically describing the key pieces of the process above. This scheme uses certificates of $O(\log^2!n)$ bits which is very good, although not optimal for every weight range.

We will describe these labels quickly, using the same example as above. In particular we will focus on the node named $I$ in the following drawing.

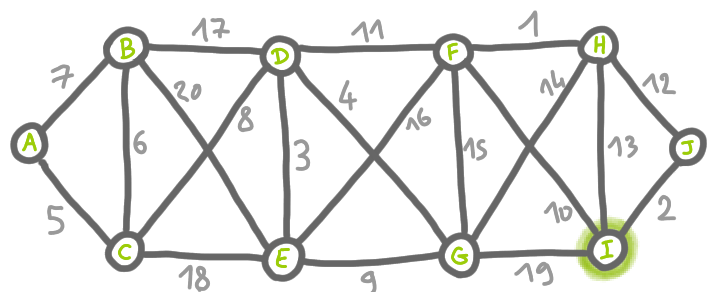
For this node, the important steps are: the merge with $J$, then the merge of the fragment $[I,J]$ with the fragment $[F,H]$, and then the merge of $[I,J,F,H]$ with $[A,B,C,D,E,G]$.

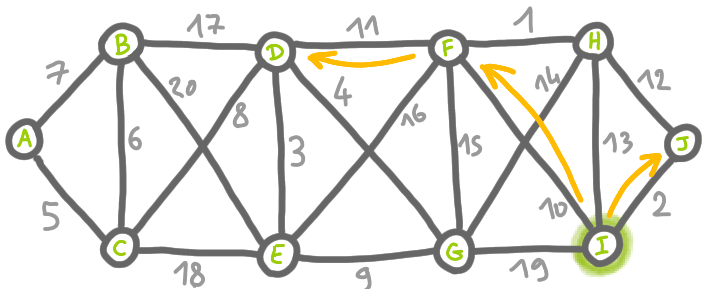
This translate into the following certificate for $I$:

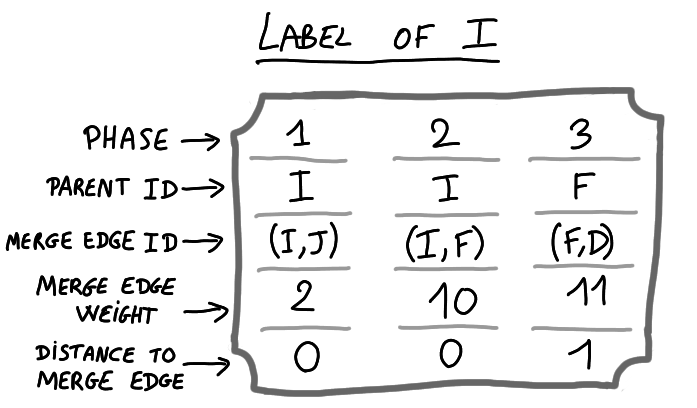
In addition to the number of the phase, and the characteristics of the merging edge, the node is given the name its “parent” in a spanning tree of the fragment pointing towards the merge edge and the distance to the merge edge. These two last pieces of information are necessary to certify the existence of a merge edge.

These certificates are enough to check that the given tree is an MST. Of course this needs a proof, but the basic idea is that the node can check that the algorithm can be executed on the graph.

This scheme uses certificates of size precisely $O(\log^2n + \log n \log W)$, where $W$ is the maximum weight. This corresponds to $O(\log n)$ phases, for which we store pieces of information of size $O(\log n)$ (IDs of nodes and distance) and of size $O(\log W)$ (edge weights).

Next post of the series.

Notes

• The paper introducing this certification is: Amos Korman, Shay Kutten, David Peleg: Proof labeling schemes. Distributed Comput. 22(4): 215-233 (2010)