Discrete notes    About    Archive

Can we always build and certify at the same time? (Maybe not.)

20 Oct 2020

This is the third and last post about building and certifying solutions, in particular for the minimum spanning tree problem. The first post is here. In the second post, we saw the classic way to build an MST in a distributed manner, using fragments. And we saw that one can build a certification of this MST during its computation. Unfortunately, this certification is not optimal for all ranges of weights. There exists another certification, that is optimal for all weight range, but it is computed after the MST.

In this post, we argue that this two-phase approach might be unavoidable.

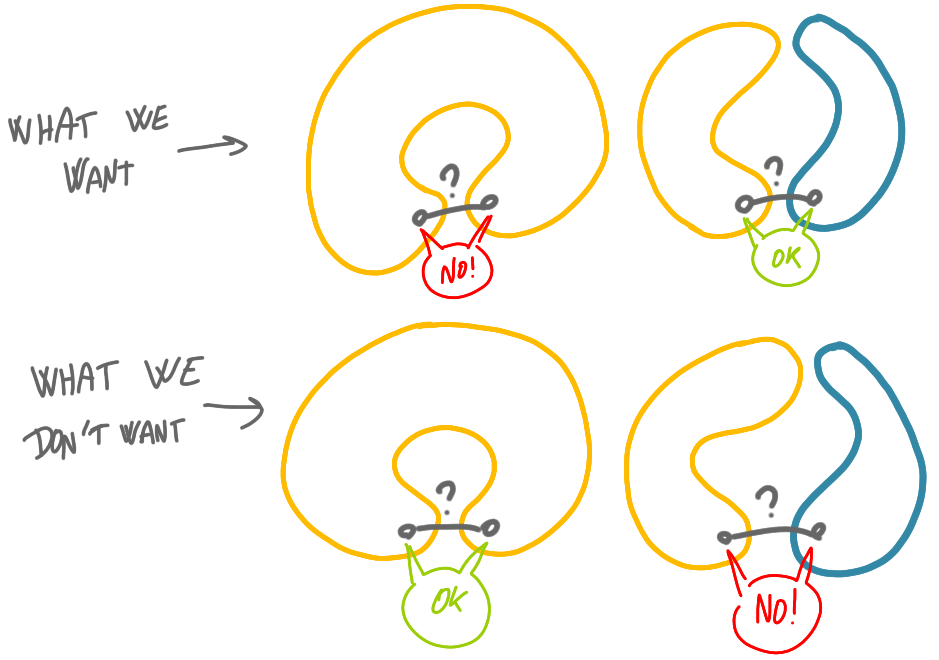
What does it mean to build and certify at the same time?

It is unclear at first what it means to build and certify “at the same time”. Indeed, any algorithm can look like a black box, that outputs the MST and its certification at the same time. One can imagine for example, an algorithm with a tentative MST, that would be certified, and only then copied in some other variables that would be the “output variables”.

As such, there might not be a good general definition for the intuitive idea that the certification is a trace of the execution. But for MST, all the classic efficient distributed algorithms that I know of build on the idea of merging fragments little by little. Then we will say that a certification is “simultaneous” if it is incremental, in the sense that after each merge, one can append a sublabel to the current certificate. At the end, the certificate should be the concatenation of the pieces associated with the different merges.

Actually, this idea can go a bit beyond MST. Basically, in the MST algorithm based on fragments, the nodes discover more and more of the graph and commit to the choice of some edges, little by little. Simultaneous certification means that every time the algorithm looks “further” it has to certify what has been done already, and this might make sense for other tasks than MST.

About fragments names

We want to show that simultaneous certification may not be possible for MST if we want the optimal certificate size. The optimal size is $\Theta(\log n \log W)$ where $W$ is the maximum weight as proved by Korman and Kutten. For small weights e.g. $W=\log n$ this is smaller than the scheme presented in the previous post, which uses $\Theta(\log^2 n)$ bits.

The reason why the previous scheme uses $\Theta(\log^2 n)$ bits is simple: a node can be in $\log n$ successive fragments, and for each of them it stores an identifier on $O(\log n)$ bits.

But why do we need these IDs? We need to differentiate between fragments because when we want to use an edge to perform a merge, it is important to be able to tell whether the two endpoints of the edge are different fragments (and then the merge is legit) or whether they are in the same fragment (and then the merge is forbidden). Taking an ID from each fragment as its “name” is an easy way to do that, as IDs are distinct by definition.

Node names in the optimal scheme

The optimal does not use exactly the same strategy of following the algorithl, but on a high level the approach is similar, and in particular the core of the scheme is a clever way to name nodes. Before we continue with our discussion, it is interesting to give some insights about these node names.

To make this more concrete, consider that the labels are built by a “prover”. The prover first looks at the tree, and chooses a node to be the center. A center should be such that if we root the tree at the center, then the subtrees have size at most half of the full tree. Here is our example from the previous post.

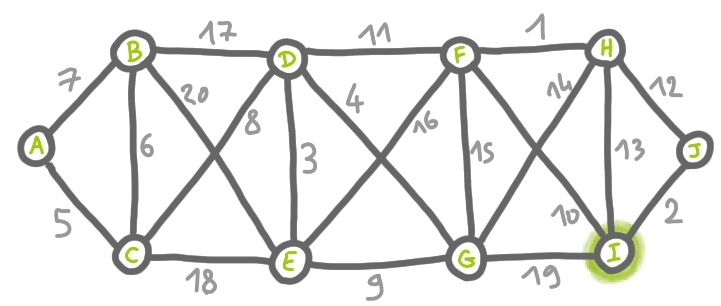
On this graph, the prover chooses D as a center. Here the subtrees have sizes 3, 1, 1 and 4, and the full tree has size 10, thus the condition is satisfied.

Now the second step is that the prover labels the $k$ subtrees from 1 to $k$, in in decreasing order of size.

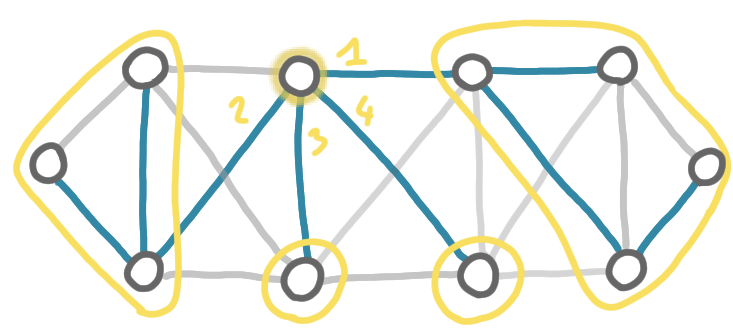
Then the same operation is repeated in the subtrees. For the subtrees of size 1, the center is obviously the only node of the subtree. For the two other subtrees, the prover chooses again a center, and labels the subtrees.

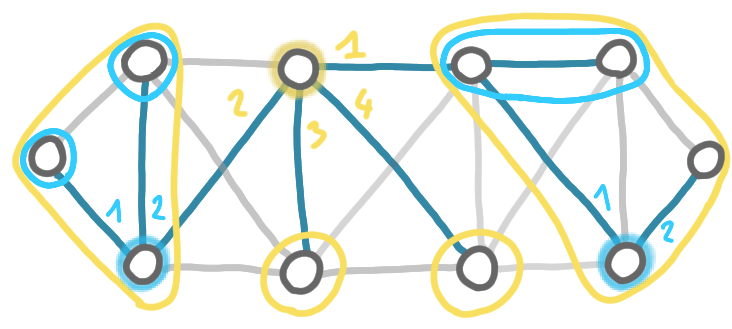
And then again for in the last non-trivial subtree.

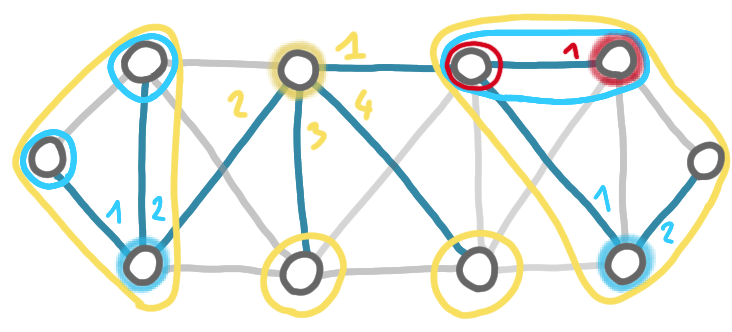
At the end, the prover assigns to each node a name that is just the concatenation of the successive subtree numbers it has received.

Why are these node names useful, checkable and small?

One can use the names to reconstruct the sequence of splits. In particular, two adjacent nodes can check at which point they were separated: it is the first position in their names were the number differs. For example on the the picture above two nodes on the right have names “111” and “12.” respectively, thus they were in the same subtree after the first split, but they were in different subtrees after the second split.

Now, this is interesting: if we consider the sequence bottom-up instead of top-down we have fragments merging instead of splitting, and the node names allow the nodes to know whether or not they are in the same fragment at that point. This is what the IDs were useful for in the previous scheme.

An important point here is that we need to check that these names are correct and that the prover does not fool the nodes. But this is easy: as in a split (or a merge when looking in the reverse direction) there is a special node, the center, that can see the name of the subtrees and check that they are different. (Given some small additional pieces of information it can also check that the numbering is in the reverse order of sizes, but let’s not go into this.)

Let’s take a look at the size of these names. First, we need to write the subtree numbers in binary. Thus at first sight, we again get some $\log^2n$ term, because each subtree number can be as large as $\log n$, and there can be as many as $\log n$ successive splits. But actually, it is known that numbering the subtrees in the reverse order of size allows to get names in $O(\log n)$ bits.

This is great: we have a technique to get compact fragment names by basically having node names that encode all the fragment names. Of course now the problem is that to choose this names we need to go top-down, with the computation of the centers etc.

Why couldn’t we get small names during computation?

Suppose we want to avoid using IDs for naming the fragments, and we want to find a smart way to assign names to the fragments. The essential part is that these names should be different.

Let us recall the two properties that we noted about the classic MST algorithms:

If we take the vanilla version of the algorithm, with these two properties, it seems difficult to get small names that can be checked. Indeed, in this case, the following scenario can occur. There is central fragment that is a long path, and at each endpoint, $k$ fragments are merging. The prover provides some names for these fragments, that are supposed to be different.

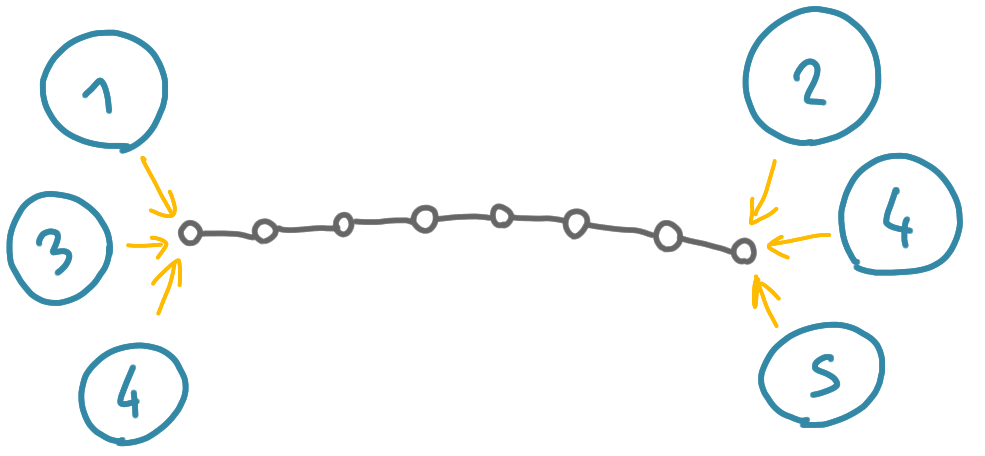
But now, how do the nodes check that these names are different? Maybe the same name is used, once on the left and once on the right. If the prover can chose arbitrary names in $[1,2k]$, then having a compact way to certify that the sets of names are disjoint is impossible. Indeed it would contradict a classic result for (non-deterministic) disjointness problem in communication complexity.

How to avoid this? One way is to force that only two fragments can merge at a time. But then the process can be slow. To see that consider a path in which the weights are increasing. At the first phase the first and the second nodes merge, but the third node cannot merge with the second and has to wait. And actually all the nodes except the first two have to wait. At the second phase, only the third node can merge etc. At the end there can be as many as $n$ phases, and then it seems hard to get small labels.

A second way to avoid the communication problem is to control better the names of the fragments. Indeed, for the communication complexity reduction to work, the names on the two sides need to be arbitrary. If we make sure that the names on the right begin with 0 and the names on the left begin with 1, then it does not work. And indeed it is easy to check that one can certify the difference between these names with a few bits. But now, remember that to get small names the optimal scheme had to use a naming related to the fragments sizes. And this would not work with the 0/1 idea: there is no reason why all the large fragments should be on one side.

So here are so elements that make me think that simultaneous certification is not possible if we want optimal size. But maybe something smarter can be done!

Notes

© 2024. All rights reserved.