Teaser for distributed certification of planarity

27 Aug 2020

A recent paper of mine, Compact Distributed Certification of Planar Graphs (here on arxiv) was presented at PODC 2020 (joint work with Pierre Fraigniaud, Ivan Rapaport, Éric Rémila, Pedro Montealegre and Ioan Todinca). Here is the link to the video by Pedro.

I was to give a teaser of it at HALG in a few days, but as I cannot be (virtually) present, here is a blog version (and Ioan kindly agreed to give the real talk).

The problem

Consider the following problem. The nodes of a graph want to know whether the graph they live in is planar. But every node has a very limited knowledge of the graph. Basically, every node can only see its neighborhood.

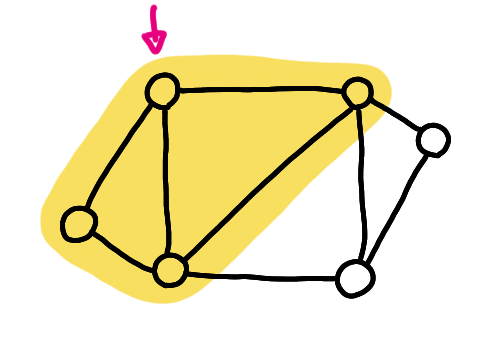
The node towards which the arrow is pointing can see only the yellow part of the graph.

More precisely, every node is equipped with a unique identifier, and knows its identifier, its degree, and the identifiers of its neighbors.

The mechanism to decide if the graph is planar or not is the following:

• if the network is not planar, at least one node should raise an alarm
• if the network is planar, no node should raise an alarm.

With a little help from a “friend”

The problem cannot be solved without help. Indeed, it could be that locally everything seems fine, for every node, but that there are “long paths” forming a $K_{5}$ for example.

The help comes as a labeling: every node is assigned a label. Theses labels can be seen by the nodes: a node can see its own label and the labels of its neighbors.

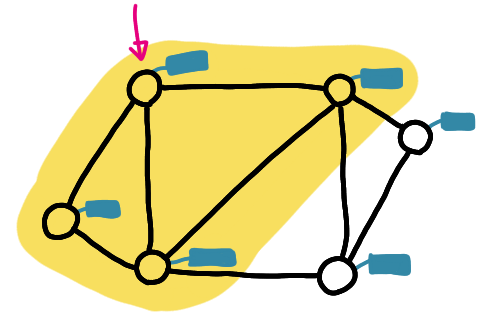
Now we want the nodes to have procedure such that the following condition is verified:

• if the network is not planar, then for all possible labeling, at least one node should raise an alarm,
• if the network is planar, then there exists a labeling such that no node raises an alarm.

Note that this condition is similar to the one of the complexity class NP.

Question and answer

It is known that for any property (not just planarity) such a procedure (labeling + rule to raise an alarm or not) exists, but the labels are large. Now the question is:

Question: What is the optimal label size?

And our answer is:

Theorem: The optimal label size is $\Theta(\log n)$.

Technique

Two words on the technique.

Things that do not work:

• Kuratowski theorem: it is not easy to certify locally that something (a minor) does not exist.
• Coordinates: if the endpoints of two edges are far away in the graph, they cannot check whether the two edges intersect or not.
• face numbering: this is more tricky, but there are examples where any local verification could be fooled if given only face and edge numbers.

What we do (in a nutshell):

• We first locally encode a transformation of the graph, where we basically blow up a spanning tree, to have an hamiltonian cycle.

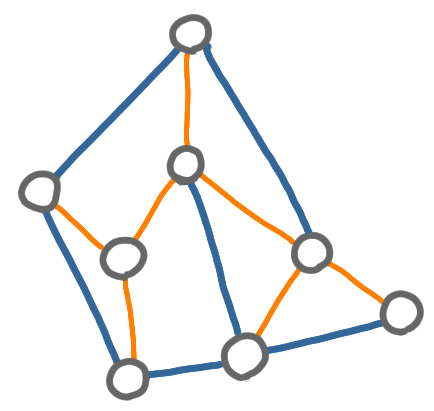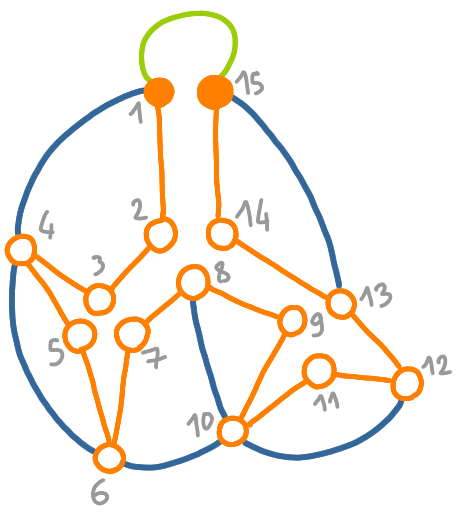• Then we use this Hamiltonian cycle to order the nodes along a line (similarly to outerplanar graphs), and then giving to every node its rank on the line is basically enough for the node to check the planarity of this transformed graph.