SSS 2020 report 1: Pulse distribution and a nice open problem

I attended SSS 2020 last week, and I’ll try to write a few posts about things I found interesting. (I’m trying to not delay too much the publication of these posts so they won’t be very deep nor polished. Comments are most welcome.)

The first post is about a problem of pulse synchronization and about the nice open problem about a “simple” discrete random process.

Austin's skyline. (The conference was supposed to be in Austin.)

Ben Wiederhake gave a nice short talk about the paper TRIX: Low-Skew Pulse Propagation for Fault-Tolerant Hardware (joint work with Christoph Lenzen). The talk video is here.

The setting is the following. It is common in computers to have several “devices” needing some common clock. A classic way to have that is to have one clock signal which is broadcast to the devices through a binary tree, like on the picture below.

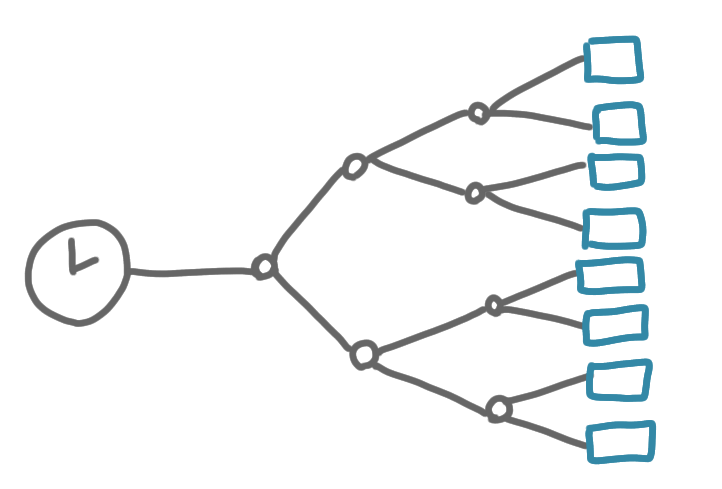
Now, if there is some abnormal delay on a link, or even a link failure, then the clocks signals received by the devices are desynchronized. The paper introduces another type of synchronization network. (The specific reasons for which this is realistic and meaningful can be found in the paper, I won’t discuss them). The authors consider a kind of generalized grid. Every node at position $(x,y)$ in the grid belongs to layer $x$, and is linked to three nodes from the previous layer, its predecessors, $(x-1,y-1)$, $(x-1,y)$ and $(x-1,y+1)$. It is also linked to three nodes from the next layer, its successors, which are $(x+1,y-1)$, $(x+1,y)$ and $(x+1,y+1)$.

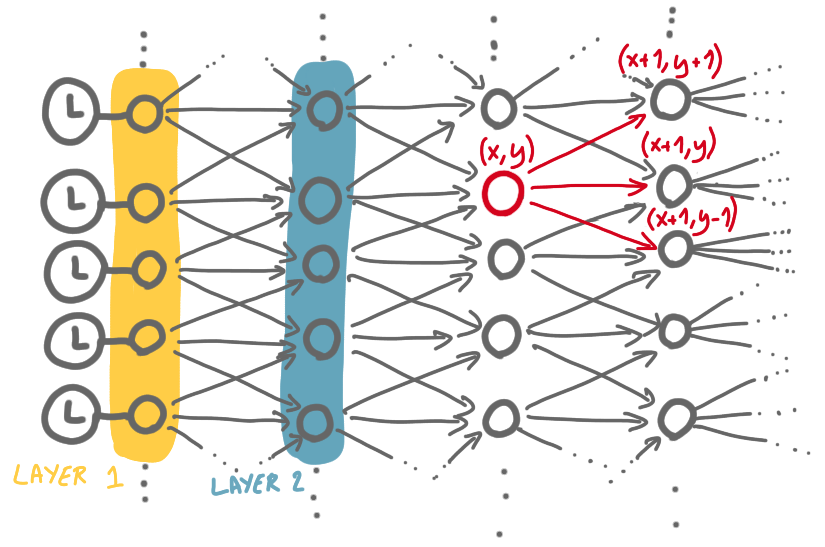
The nodes of the first layer are synchronized, and send a pulse at the same time. The key point is that every node sends a pulse to its successors when it has received the pulse from two of its predecessors. This ensures a kind of fault-tolerance: if a node has crashed, then the synchronization can still happen perfectly, as its successors will still receive two pulses.

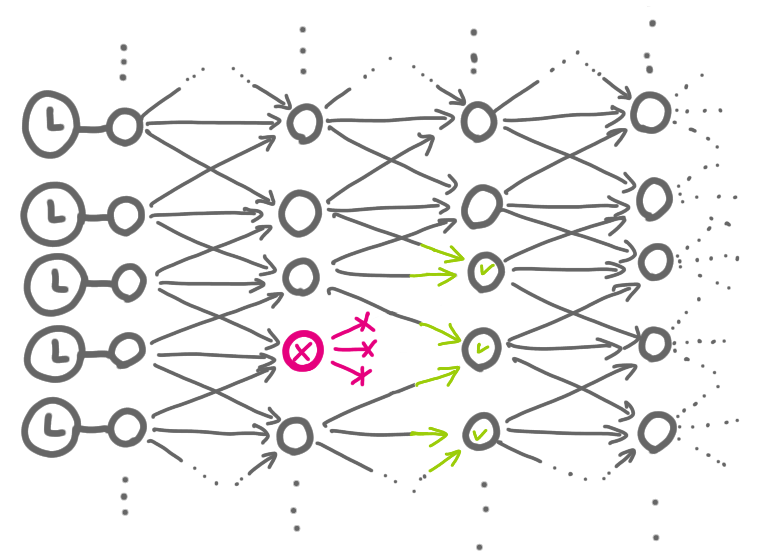
But what the authors focus on is the skew between pulses of different nodes. Because the wires are not perfect, it can take some time $\tau_1$ for the signal to go from one node to one of its successors, and time $\tau_2$ to go to another successor. Now a question is, with this grid-like structure, how much difference can there be between pulses at different nodes?

To get a more precise and clean question, the authors consider that with probability 1/2, the signal traverses the link in time 0, and with probability 1/2 it traverses the link in time 1. And they focus on the following question: given two nodes of the same layer, that are adjacent (e.g. some $(x,y)$ and $(x,y+1)$), what is the difference between the times at which they receive the signal? (This difference is called the skew.)

The authors show by numerical experiment that the maximum skew at some layer $H$ is lower than $\log \log H$. They also have other statistics showing that the skew is very concentrated etc.

The obvious question from a TCS point of view is: can we show good bounds on the process? This seems very hard. Already in 2018, the authors mentioned the problem at the Helsinki February workshop, and could not get good bounds. One of the reason why this is difficult is that at each node some input is lost: if the three pulses arrive at time $t$, $t’$ and $t’’$, then the node “fires” at time $t’$, and does not care about $t’’$. In some sense $t’’$ is lost.