Popular matchings

Popular matchings are a nice variant of the classic stable matchings. In this post introduce these matchings, and give some bits of information about them.

Stable matchings

Remember what a stable matching is. There is bipartite graph, where every node holds an ordering of its neighbours, known as the preference list. A matching $M$ in this graph is stable, if no edge $(u,v)$ that is not in $M$ is such that both $u$ and $v$, would prefer to be matched together instead of the way they are matched (or unmatched) in $M$. Note that such matchings are maximal.

A stable matching always exists and can be computed in linear-time using the famous Gale-Shapley algorithm. Something frustrating with stable matchings is that they may be small with respect to the maximum matching (if one forgets about the preference lists). For example, in the following picture, the stable matching matches the top node on the left, with the bottom node on the right, and prevent the two other nodes from being matched, although all could be matched.

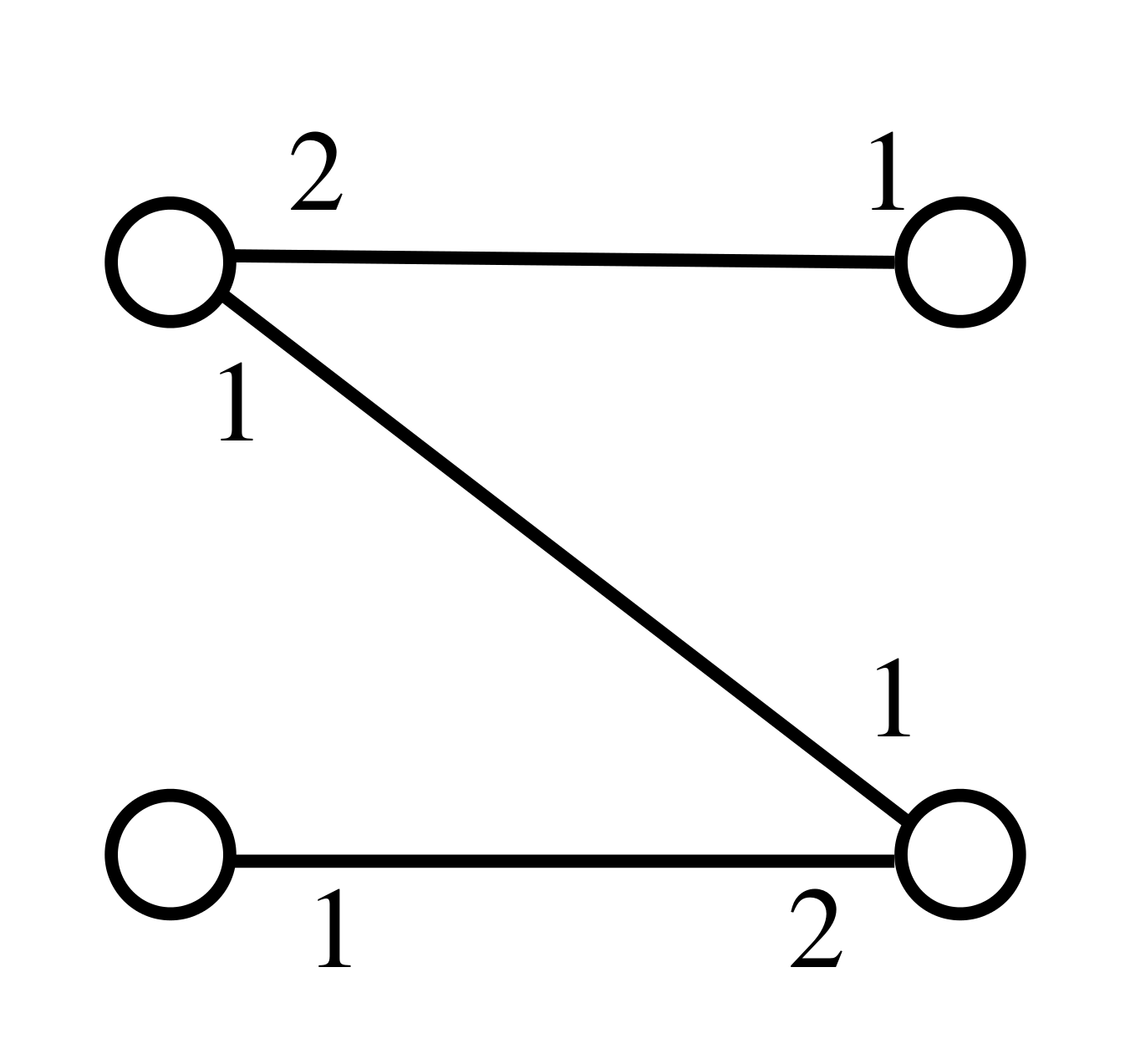
This example shows that the size of a stable matching can be half of the size of a maximum matching. If you are in a context where you would like to (at least partially) satisfy the nodes in terms of preference lists, but you would also like to satisfy as many nodes as possible, then you need another form of optimality, and (max-size) popular matchings is a good one.

Popular matchings

With a stable matching the matched nodes are happy, because they are at a kind of equilibrium, but the other nodes are unhappy because they are not matched at all. What happens if you make the nodes vote for their favourite matching? This makes sense if you do a tournament: for every couple of matchings you make an election, and the winner is the matching that is prefered by the majority of the nodes. In such an election the vertices perfer to be matched, and if matched consider their preference list. Also if there is an ex-eaquo then both matchings win. A matching is popular if it wins every election.

Relation with stable matchings and size considerations

It is known that every stable matching is popular. Thus popularity is a relaxation of stability. Unlike stable matchings, popular matchings can have different sizes, and in particular they can be larger the stable matchings (that why we look at them in the first place). Actually, stable matchings are the worst popular matchings with respect to size: stable matchings are the popular matchings of minimum size.

We then look for max-size popular matching. The good news it that a max-size popular matching can be computed in polynomial time, and that they have size at least 2/3 of the maximum size matching.

Notes

I got aware of this topic at a seminar of Telikepalli Kavitha at IRIF in September. After a nice introduction, she told us about her recent papers on the topic (there is a lot to say, with many relevant variants and nice algorithmic techniques).

The concept of popular matchings was introduced by Gärdenfors in the seventies, who also proved that stable matchings are popular.¹ The polynomial algorithm for computing a max-size popular matching is much more recent, it was designed by Telikepalli and Chien-Chung Huang in 2011.² And popular matchings are still a hot topic.³

Footnotes