Perfect matchings with optional vertices
02 Mar 2023This post is about a simple problem related to matchings.
The problem
Consider the following problem, that I will call perfect matching with optional vertices.
Input: A graph $G=(V,E)$, and a subset of vertices $S\subset V$.
Question: Does there exist a matching of $G$ such that all the vertices in $V\setminus S$ are matched?
In other words, you look for a relaxed perfect matching, where it is ok that some vertices are unmatched if they belong to $S$. I call $S$ the set of optional vertices.
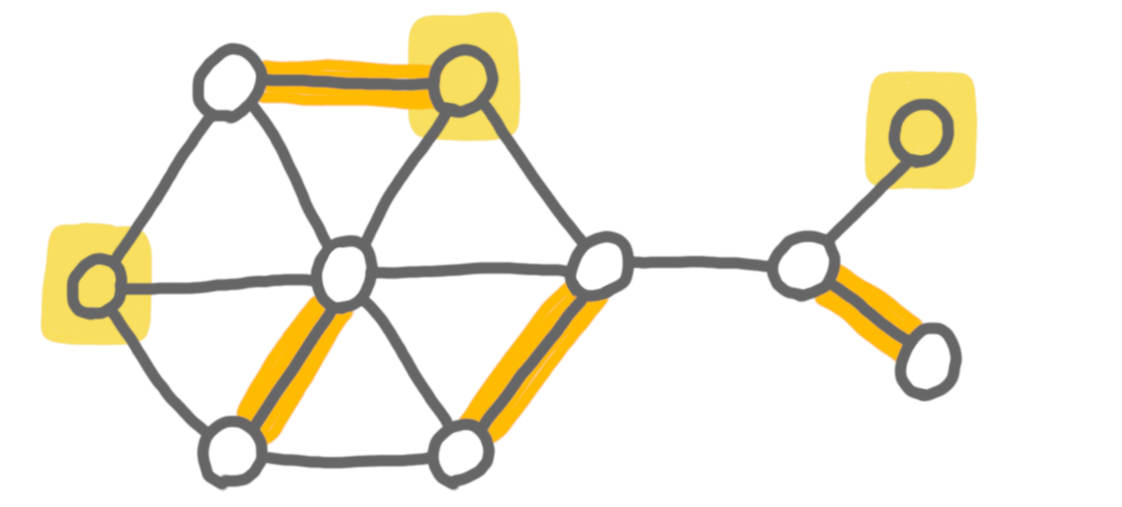
For example, here is a graph with optional vertices in yellow, and a solution in orange.
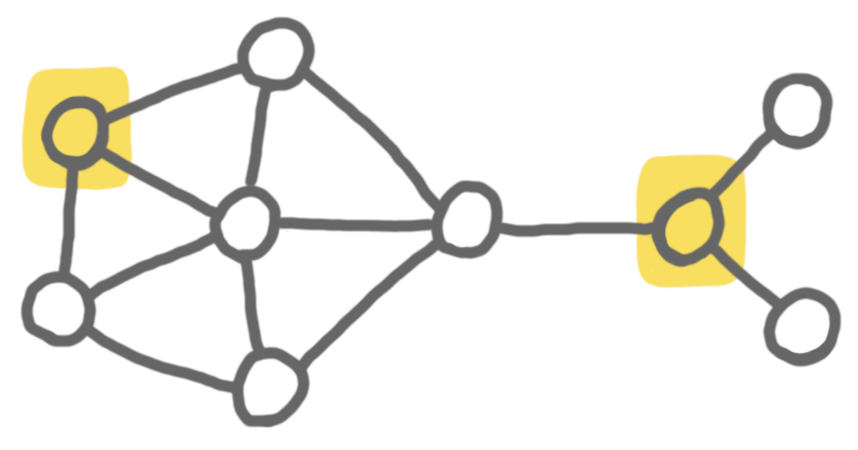
And here is an instance that has no solution (because both vertices on the right have to be matched, and this is impossible).
What is the complexity of this problem? Is it polynomial because it ressembles perfect matching, or is it NP-hard because you somehow have to enumerate all the possible subsets of $S$? If you like algorithms, maybe you want to take a few minutes to think about it.
A solution
I came up with this problem while studying some notion of robustness, in the spirit of this paper. And I immediately thought about asking Nicolas El Maalouly a PhD student at ETH Zurich I had met a few months before, who is a specialist of matchings. And he very quickly answered with the following neat algorithm. Thanks again Nicolas for this!
The answer to the complexity question is that it is not harder than perfect matching. Actually, there is a very efficient reduction to perfect matching.
Assume first that the graph has an even number of vertices. We create a new graph $G’$ by adding all the missing edges between the optional vertices, like on the drawing below.
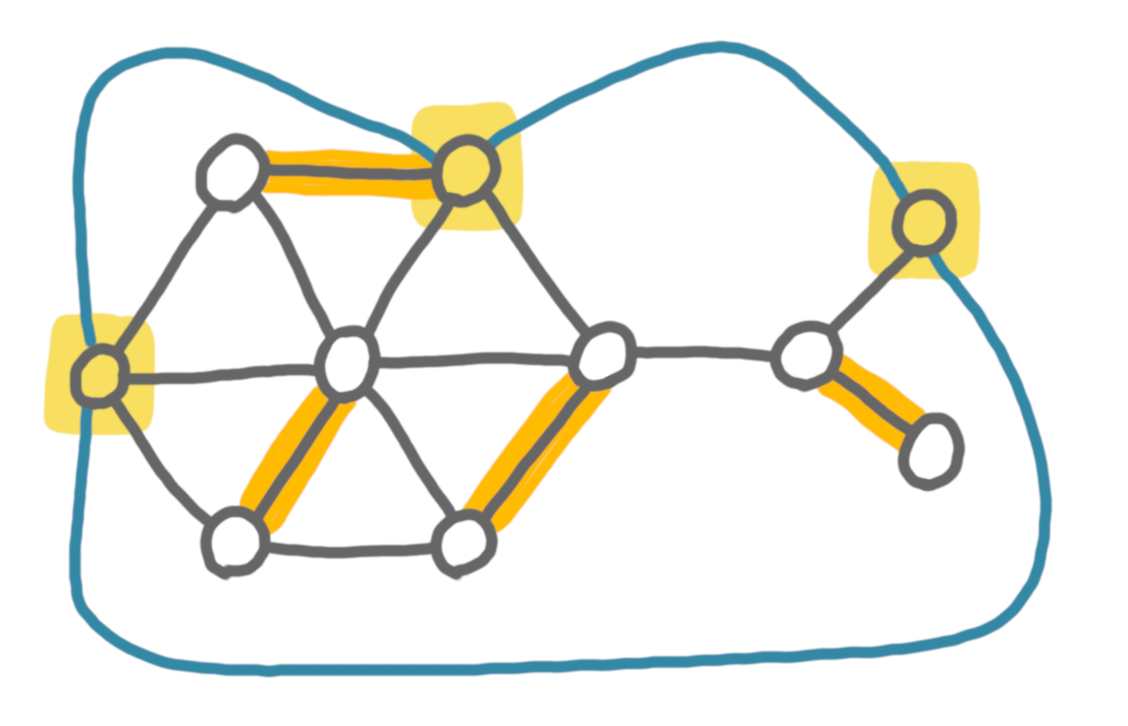
Then we run a perfect matching algorithm on $G’$. If a perfect matching exists in $G’$, we can simply remove the edges we just added, and get a perfect matching with optional vertices of the original graph $G$. Now, for the reverse direction, if a perfect matching with optional vertices exists in $G$, then there is a perfect matching in $G’$: just pair the unmatched optional vertices two by two (which is possible since $G$ has an even number of vertices), and add these edges in the matching.
Now if $G$ has an odd number of vertices, we first add a new optional vertex, and then we add the missing edges to have a clique of optional vertices, like on the drawing below.
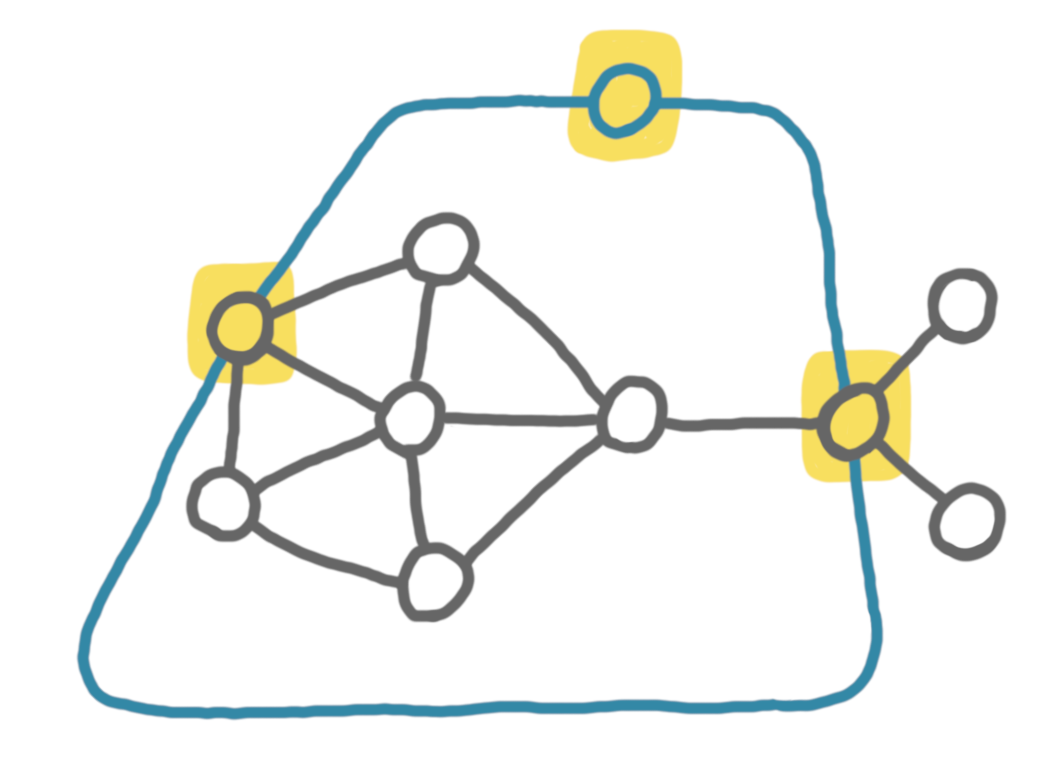
Now the same kind of reasonning holds.
(I guess this was known before, but I couldn’t find a reference.)