Graph reconstruction conjectures
04 Oct 2024Last week I attended an online talk by Paul Bastide about graph reconstruction. In this post I will follow closely the structure of the first part of his talk, surveying open problems in the area. If you interested, the video is available online here (with suboptimal sound), and also contains the second part where Paul speaks about his nice work on related problems.
General approach
Graph reconstruction is about reconstructing a graph (or at least deciding if it has a given property) given a collection of partial views of it. In other words, one makes queries to a hidden graph $G$ (for various types of queries) and tries to output the hidden graph, or determine whether $G$ satisfies some property. Sometimes the question is whether this is possible at all, and sometimes the goal is to determine the minimum number of queries needed.
This has a similar flavor as graph property testing (making queries to a hidden graph), but there is no epsilon: you want to reconstruct the graph (resp. decide the property) exactly and deterministically.
In the following, I discuss quickly the three conjectures that Paul highlighted in his talk. They use three different types of queries: edge queries, deck queries and line queries.
Evasivness conjecture
The most natural type of queries one can think of is: Is (u,v) an edge of the graph? This is an edge query. To be able to ask the question, one needs to know the names of nodes, and here we can assume that they are between 1 and $n$, for a known $n$. We will try to minimize the number of queries, for the worst name assignment.
Now, one would like to prove statements of the form “deciding if the graph is planar can be done in X edge queries”. And at first, this seems hopeless and uninteresting. Indeed, deciding whether the graph is empty takes $n(n-1)/2$ queries, the trivial upper bound. But it is not true of every property. For example, deciding whether a graph is a scorpion graph can be done with $O(n)$ queries. The picture below describes such graphs. The proof is non-trivial but shortish, see e.g. here.
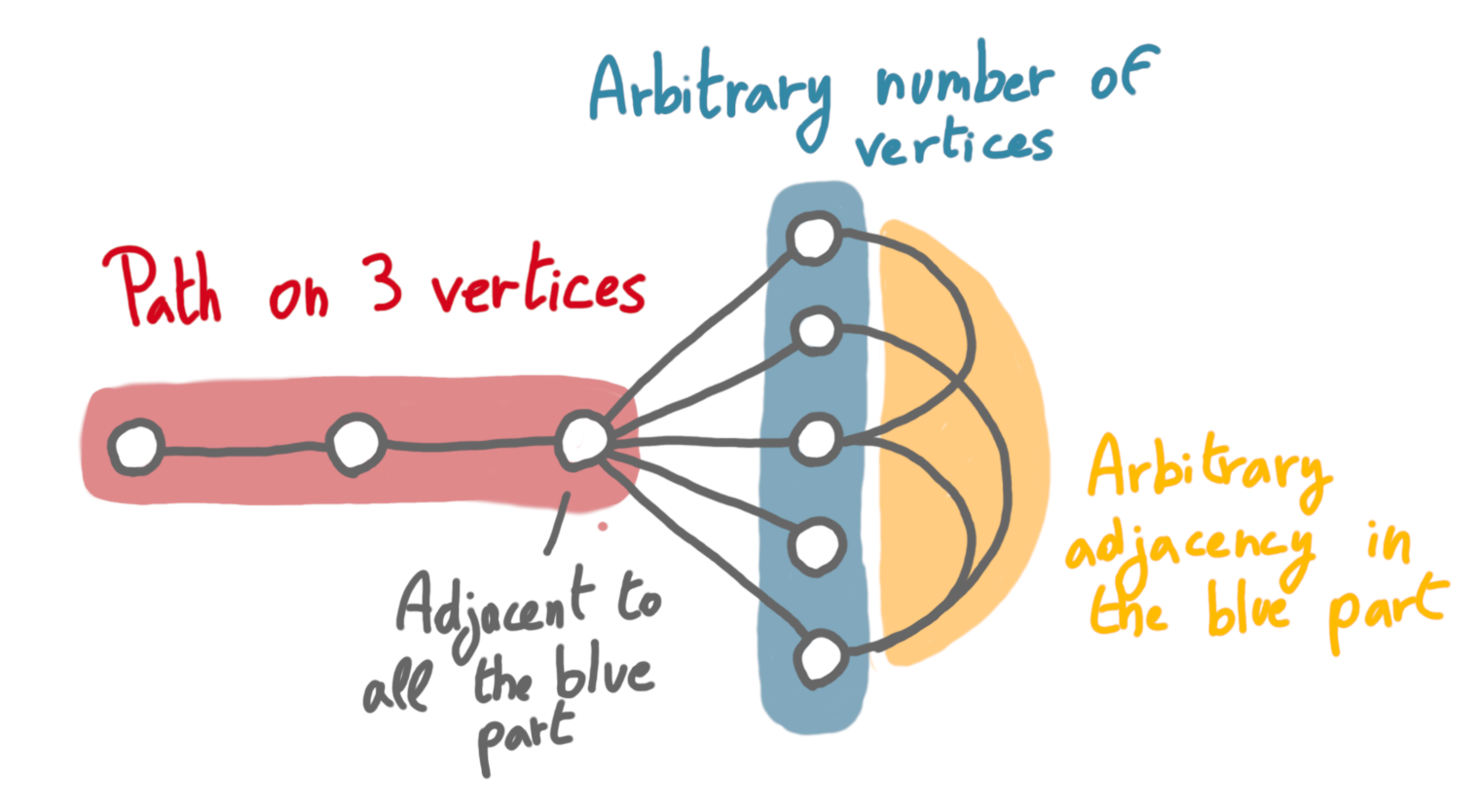
Being a scorpion graph is not a monotone property: it does not stay true when one removes edges. (It seems that “monotone” refers either to removing or to adding edges, depending on the author, but here it doesn’t matter.) The Evasivness conjecture states that for all monotone graph property, the edge query complexity is the trivial $n(n-1)/2$. It is also known under the name of Aanderaa–Karp–Rosenberg conjecture.
There has been a series of papers proving that $c \cdot n^2$ queries are needed, for larger and larger $c$, the current best being $c=1/3$. The conjecture has been proved when $n$ is a power of a prime, by studying “group actions on topological spaces” .
Reconstruction conjecture
Consider now a new setting. One is given access to the deck of the hidden graph $G$, which is the multiset of all the graphs that can be obtained by removing exactly one vertex from $G$ (the cards). On the picture below, the hidden graph is on the left and its deck on the right. Note that for this setting it is important that the vertices do not have no names.
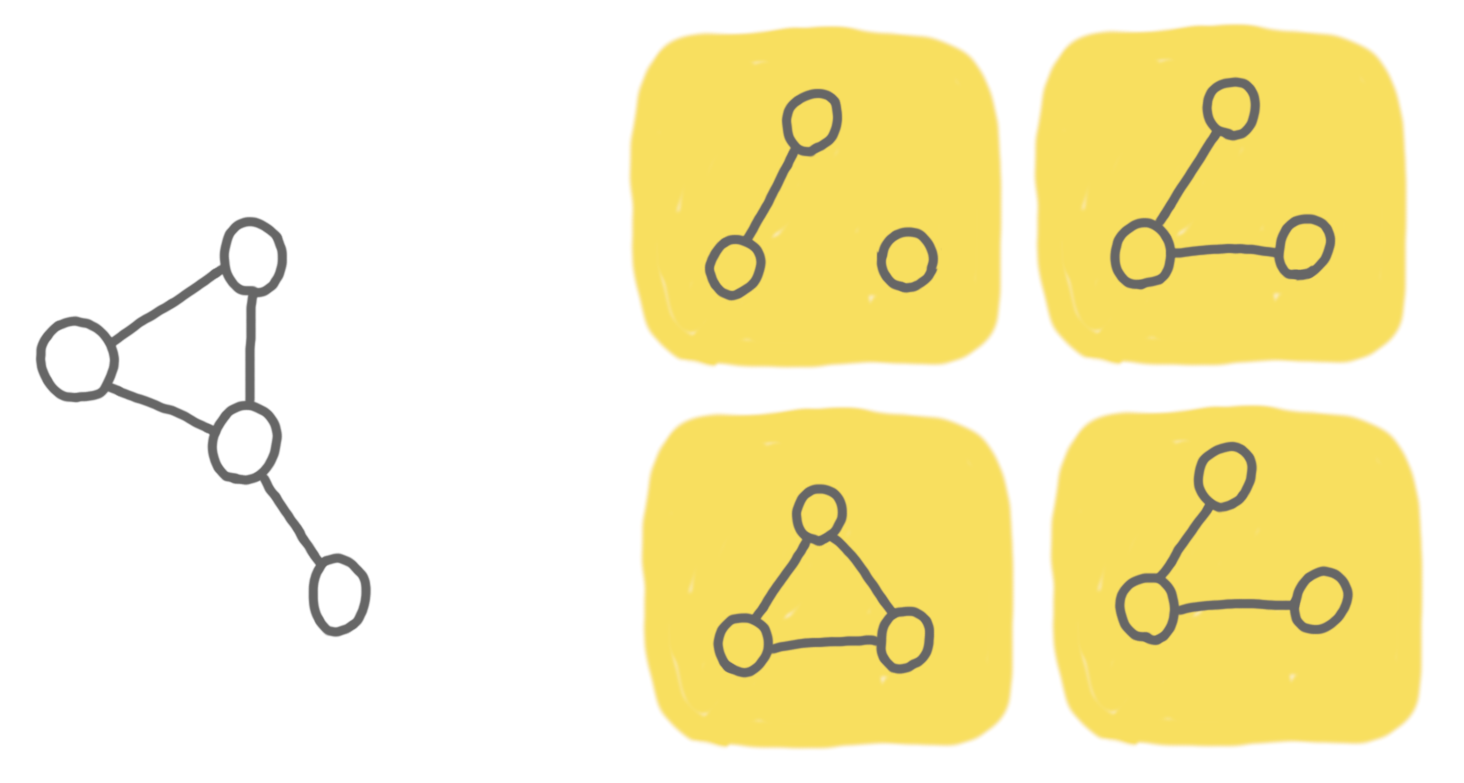
It’s not clear how to reconstruct the original graph from the deck, because of all the symmetries. (Try to imagine what you would have done with the deck above.)
The reconstruction conjecture states that it is always possible to reconstruct a graph from its deck (assuming $n>2$, an edge and two isolated vertices having the same deck).
The conjecture has been proved for various graph classes, such as trees and outerplanar graphs.
Graham tree reconstruction conjecture
A less known conjecture is Graham tree reconstruction conjecture. (The only reference I could find online is here, but it seems to be well known in the reconstruction community.)
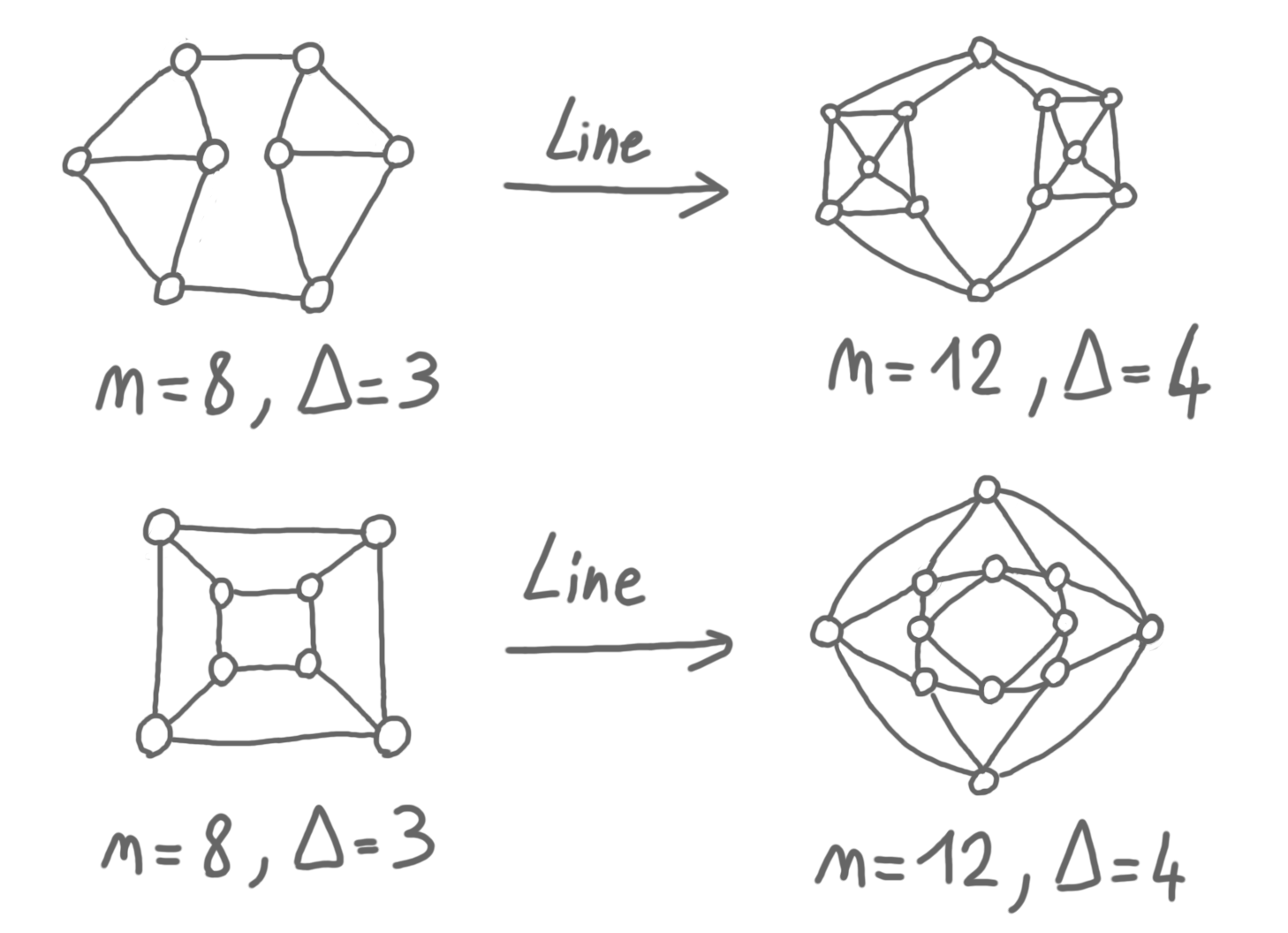
It is based on the notion of line graph. Given a graph $G=(V,E)$, its line graph is the graph $L(G)$, with vertex set $E$ (one vertex for each edge of $G$), such that $(u,v)\in L(G)$ iff $u$ and $v$ correspond to edges that share an endpoint in $G$. See the picture below.

If we iterate this operation, we get larger and larger graphs, in general, and the sequence $|V(G)|, |L(V(G))|, |L(L(V(G)))| …$ increases rapidly.
The question is: Is it the case that this sequence characterizes the original graph $G$? In general, this is not true, because two $k$-regular graphs of size $n$, have the same sequence (see the picture below for one step). But Graham conjectured that this is true for trees.
All these three conjectures are still wide open.