Notes for (rainy) May

11 May 2020

Notes for May.

A picture from May 2020.

Active learning and interactive protocols

The Grace Murray Hopper Award has been given to Maria Florina “Nina” Balcan for her work in machine learning. One of her contributions is in active machine learning.

In a classic setting of machine learning, the machine is given a lot of labeled data and must produce a classifier: an algorithm that can guess the label of a new data point. In active learning, this is made interactive: the machine can create a data point and ask for the label of this point. For example in the following picture, in order to have a good classifier based on the red and blue points, the machine may ask about the yellow points, to know which hypothesis is the best between the green and the pink one.

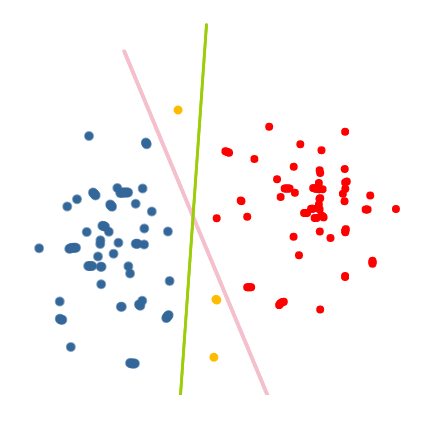
A reason to do that is to save time: after processing a fraction of the data, the machine can have some preliminary idea of what the classification looks like, and only relevant data points at the boundary of this partition are really useful. Another reason is if the data points themselves are costly. I remember a talk¹ where the goal was to decide whether small islands close to the shore reduce or increase the damages of a tsunami. If you have perfect knowledge of the dimensions of your island, you can run a precise fluid simulation, and that’s it. But if you want a big picture of whether islands in general are bad or good, then you would need to run many simulations, and you cannot because it takes too much time. Then you can use machine learning to get an approximation of the damage as a function of parameters of the island. But remember that any new point takes ages to be computed, thus you would like to have only useful data points in you learning set. And somehow you cannot always select your points a priori ; then having active learning is great.

Balcan basically proved that active learning can be efficient even in the presence of (all kinds of) noise. The Hopper award laudatio cites two other key works, in semi-supervised learning and clustering.

[I learned about this in a post on Lipton’s blog, that contains the following amusing sentence: “Active learning follows a classic idea in computer theory: Making a protocol interactive can often decrease the cost, and almost always makes the protocol more complex to understand”.]

Sprouts game

Images des maths a maths popularization website in French has an article on sprouts, a combinatorial game related to planar graphs.

It is a paper and pencil game between two players. They start from an arbitrary set of points, and then play one after the other. At her turn, the player has to do two things:

• draw a line between two points (including self-loops)
• draw a point on this line (not at one of the end points)

and there are a few constraints:

• the lines should not intersect
• every point has degree at most three.

At some point one the players cannot play anymore, this player looses. On the following picture, there are three initial points. The blue player makes the sixth move, and after that the red player cannot play. Therefore the blue player wins.

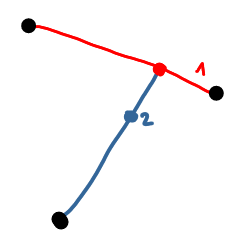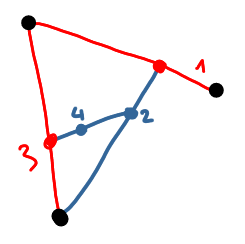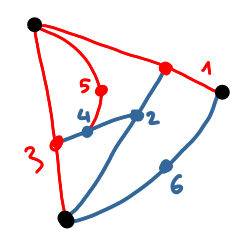Researchers have completely characterized what are the winning strategies for this game up to 44 initial points. And there is the following conjecture: if both players play perfectly, the first player cannot win if and only if the number of initial points is 0, 1 or 2 modulo 6…!

Diffraction and algorithms

The other day, there was a paper on the arxiv named Algorithmic Foundations for the Diffraction Limit and I thought that “diffraction” had a meaning that I didn’t know about, outside of physics. So I looked at the abstract, and actually it’s about the good old optical diffraction!

From what I understood (and remember) here is the topic of the paper. When you have two sources of light far away one from the other, and you observe the diffraction image created by a circular aperture, you can say “yes there are two sources of light, and they are in that position”. But when the two sources are close one from the other it’s less clear. It is believed that there is a fundamental barrier after which you cannot decide between one and two sources. There are several criteria to decide where this barrier is, with various explanations but all are heuristics.

The approach of the paper is to consider that one receives the diffracted image through (noisy) samples, and based on this samples must decide whether there are one or two sources. This becomes a more statistical problem, and when we ask how many samples are needed, then it becomes more algorithmic too. Then one can design algorithms with a complexity depending on the number of samples, the noise etc.

Trusses

In the study of social networks, a classic topic is to understand and detect communities. In terms of graphs, the simplest object representing a community is a clique. But this is a very demanding definition: there are many groups that one would call a community, where not everybody knows everybody. A classic alternative here is a $k$-core. A $k$-core is a maximal connected subgraph, with all nodes having degree at least $k$ in this subgraph. That is everybody should know at least $k$ other members.

I learned recently about another such object: $k$-trusses. A $k$-truss is a maximal connected subgraph, such that inside this subgraph, every node is adjacent to at least $k$ triangles. So now you want that every person can cite $k$ pairs of acquaintances who know each other. It’s a more restricted notion than $k$-cores, because in some sense the communities must be more “local”, with each neighborhood being more connected.

[I learned about this while taking a look at the papers published in JGAA journal for the post about journal fees. The paper in particular is this one, which discusses bounds and algorithms for $k$-trusses.]

Eggs and reconfigurations

The Aperiodical has an article about a maths game, with a box of eggs. The game is the following. You start with a box of eggs in this configuration:

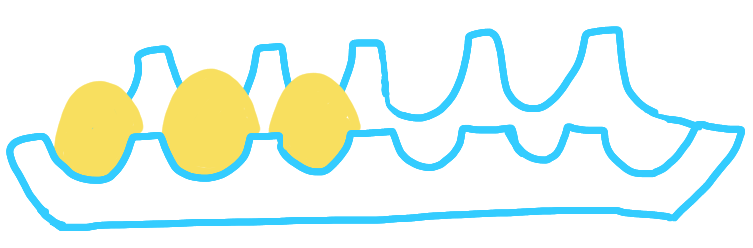
and you should transform it into that configuration:

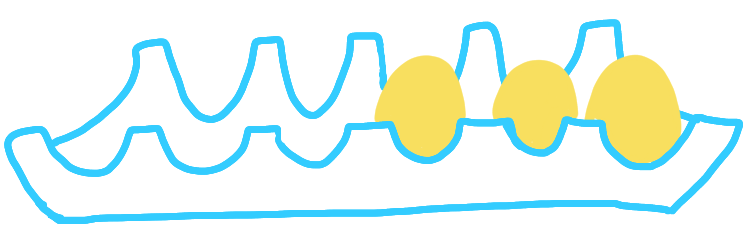
using only movements of the following form (move one right):

The question is what is the minimum number of moves? In general I would consider this as just one more maths game, but as I will be working on reconfiguration problems next year (in Lyon with Nicolas Bousquet), this is relevant. Reconfiguration problems are problems of the form: how to get from configuration A to B in the minimum number of moves of some sort. This is important for example for random generation of solutions to combinatorial problems.

Other notes

• The Simons institute launches a new series of video, “Theory shorts”. The first one is about vision and brain ; quite interesting.

• An interesting blog about algorithmic fairness that I didn’t know: Algorithmic fairness.

• In a “vidcast”, Gasarsh and Fortnow talk about conferences. In particular, about having conferences sometimes in person, sometimes virtual (and also about regional conferences). Incidentially, they mention the fact that the conference accronym EC used to be for Electronic Commerce, which is weird… (now it’s Economy and Computation which makes more sense).

• I realized that the blog was hard to read on smartphone because of the format of the pictures, it should be better now.

• I started making pictures with my tablet, and it’s a very good solution. Before looking into it, I didn’t know one could have a simple software with layers and opacity parameters on tablets. It’s especially nice to have a first sketch, and then make a precise drawing. I use it not only for the blog but also for picture prototypes in manuscripts.

Footnotes