Notes: Graph-related stuff

30 Apr 2021

Some notes on graph theory topics.

A picture from April 2021.

Linkless embedding, a generalization of planar graphs to three dimensions

Planar embedding are embedding of a graph in the plane without crossing of edges. Only planar graphs have such embeddings. If one goes to three dimensions it is easy to avoid edge crossing, for any graph. But there is a meaningful generalization of planarity to 3D, which is linkless embeddings.

A linkless embedding, is an embedding of a graph in 3D such that no two cycles are “linked”. I found no easy way to describe this notion with words so I’ll just make a drawing (the important part is highlighted in yellow).

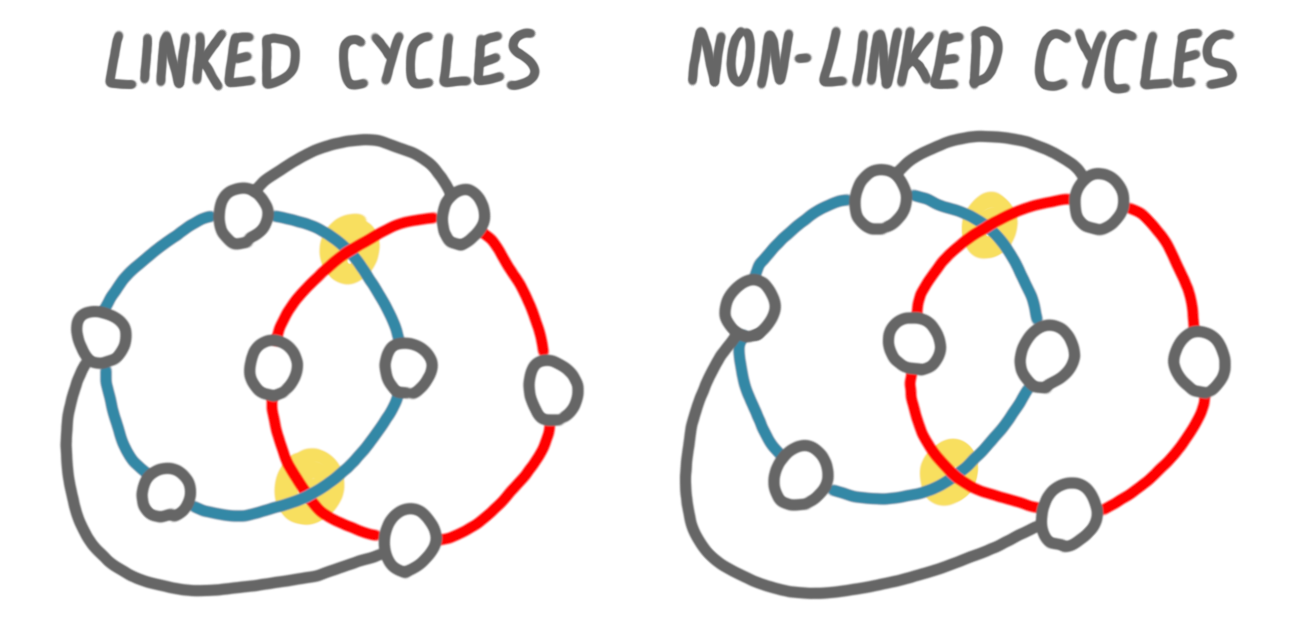
I discovered this notion (along with other things) in the blog post Ten things you (possibly) didn’t know about the petersen graph. Petersen graph, and in general the Petersen family are archetypes of graphs that do not have a linkless embedding. One of these graphs is $K_6$, the clique on 6 vertices. Below is an attempt at building a linkless embedding for $K_6$, that unsurprizingly fails.

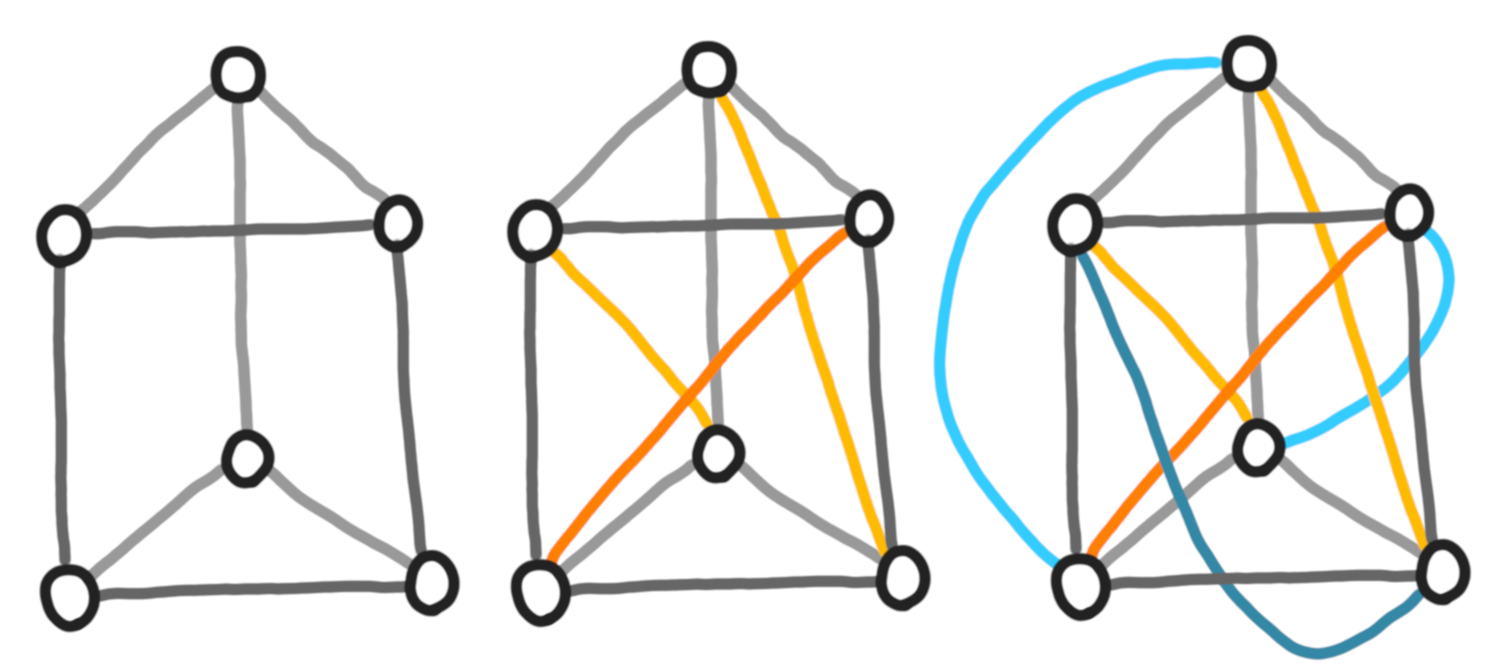
Constructing a $K_6$ little by little. First the gray edges (the clique minus two matchings), then the orange edges (one matching) and then the blue edges (the other matching).

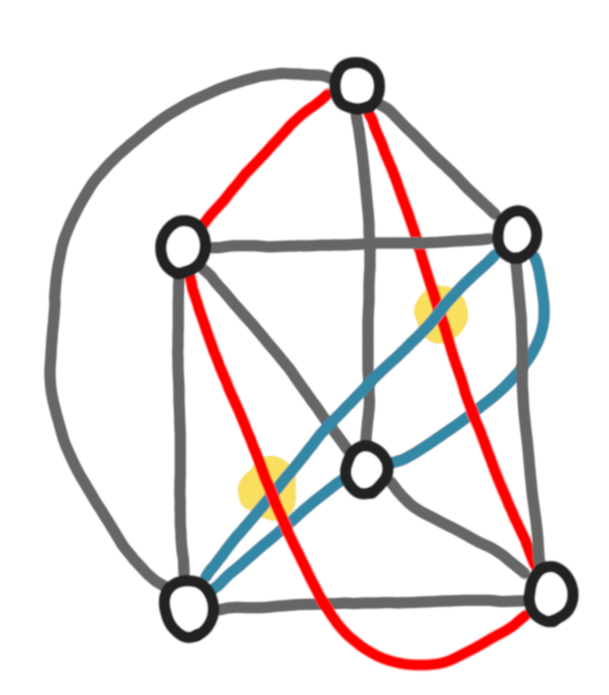
The same embedding, but now with two linked cycles highlighted.

Pointer to JCRAALMA

A few weeks ago was the second edition of JCRAALMA a French 3-days workshop (in English) on a graph theory topic. This year the topic was width parameters (treewidth, cliquewidth, and all their friends). Because I had to prepare for a job interview I didn’t attend, but I plan to catch up in the months to come. The videos are available on that webpage.

Actually I didn’t attend last year either, but I learned a lot from the few recorded talks I watched. (The next two notes come from the first 15 minutes of the first talk by Gwenaël Joret.)

I think the format is very nice: around 10 one-hour online talks, spread on three days, with a meaningful schedule (a precise topic per day, and increasing difficulty, starting from scratch in the first talk and finishing with cutting-edge research).

Small separators = small treewidth

If you know the notion of treewidth, you probably know that having a small treewidth implies having a small (balanced) separator.

You might not know that in some sense the converse is also true. Dvořák and Norin proved (paper) that if every subgraph of a graph $G$ has a balanced separator of size $a$, then $G$ has treewidth at most $15a$.

Baker’s technique for peeling planar graphs

Baker’s techniques (named after Brenda Baker) is a way to decompose planar graphs. Basically it’s about peeling the graph like an onion, by iteratively removing layers.

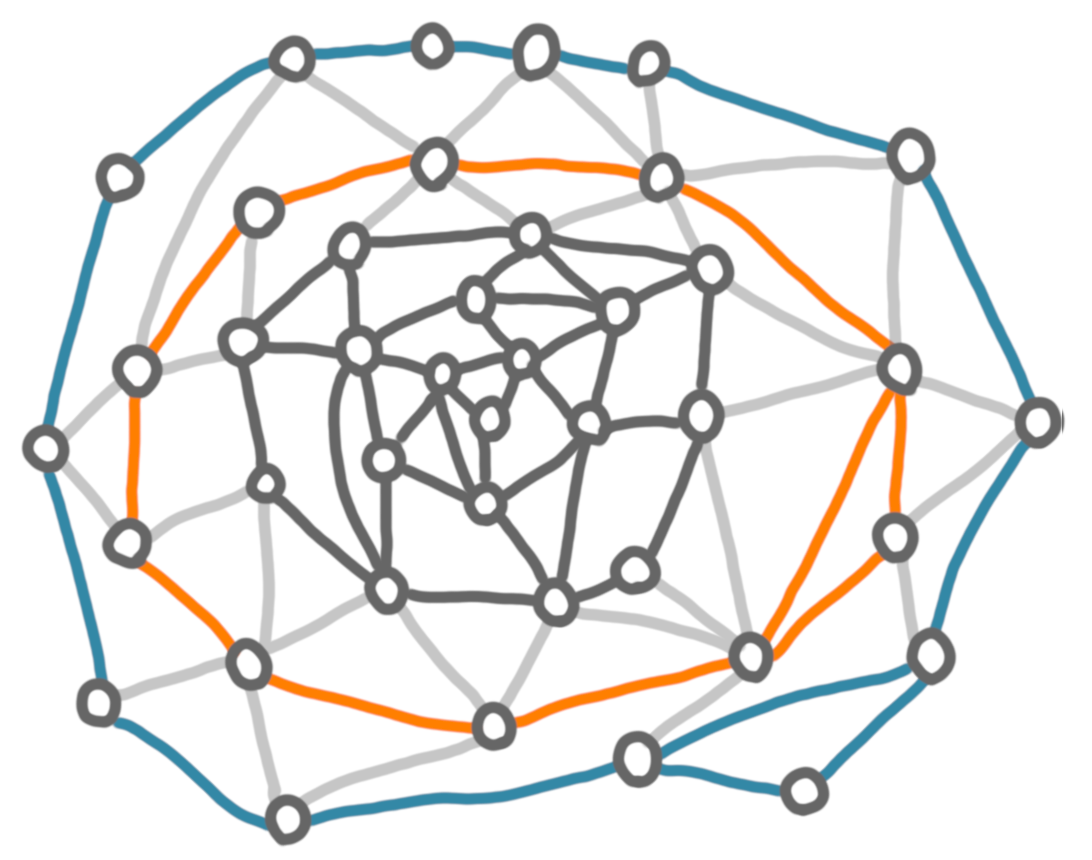
Let’s make an example. Consider the following graph.

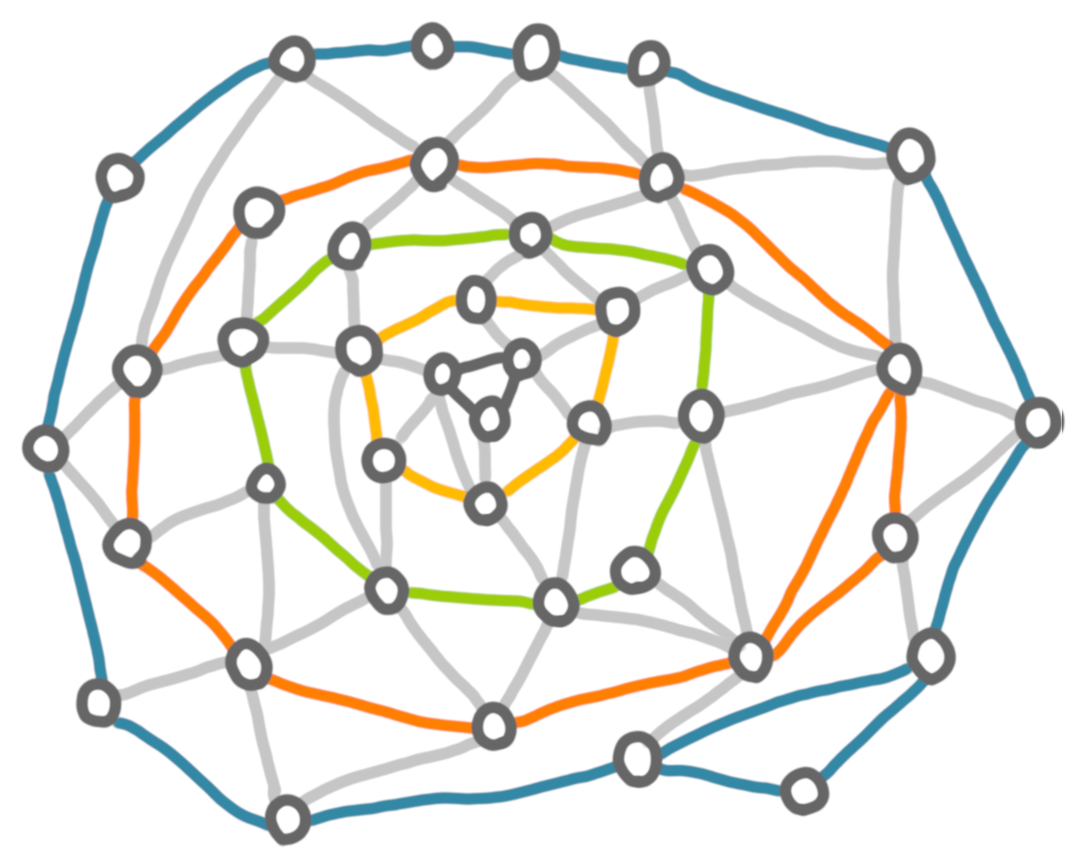
The first layer is the nodes that are on the outerface, plus the edges between these nodes. For the next steps, we can forget about the edges that have exactly one endpoint in the layer (depicted in light gray in the picture).

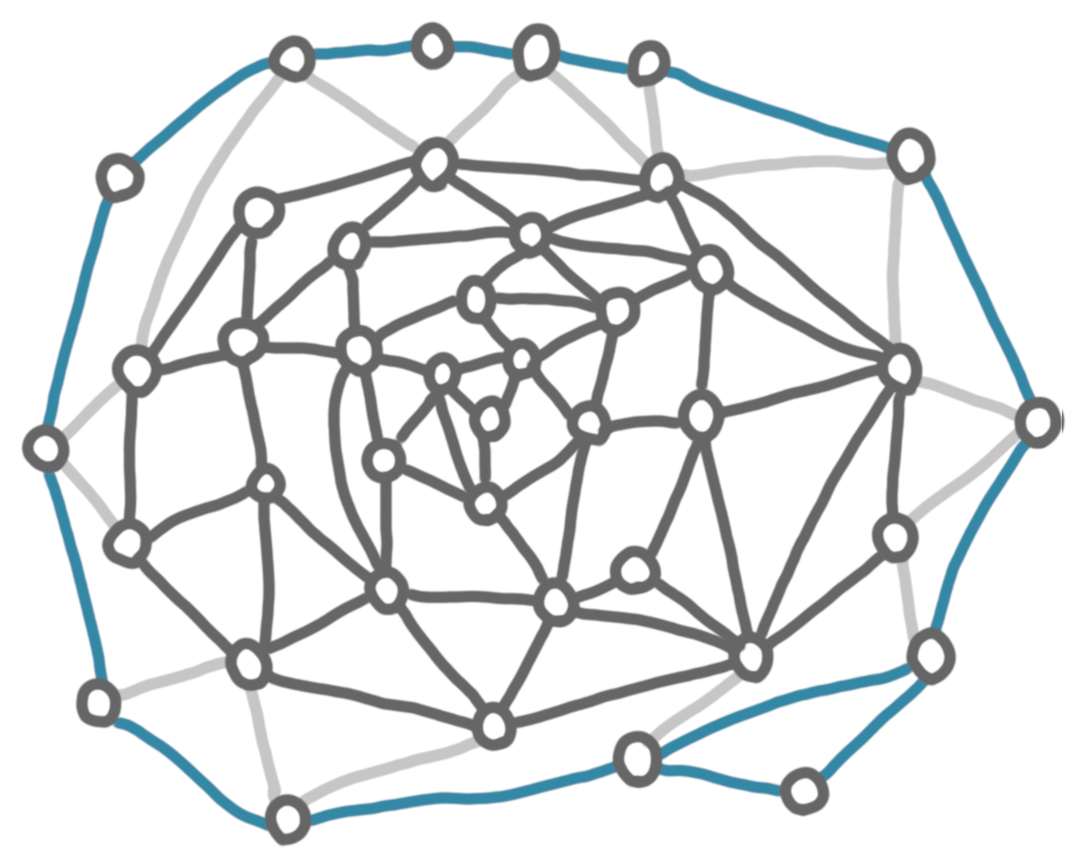
Now we repeat the process until every node is in a layer.

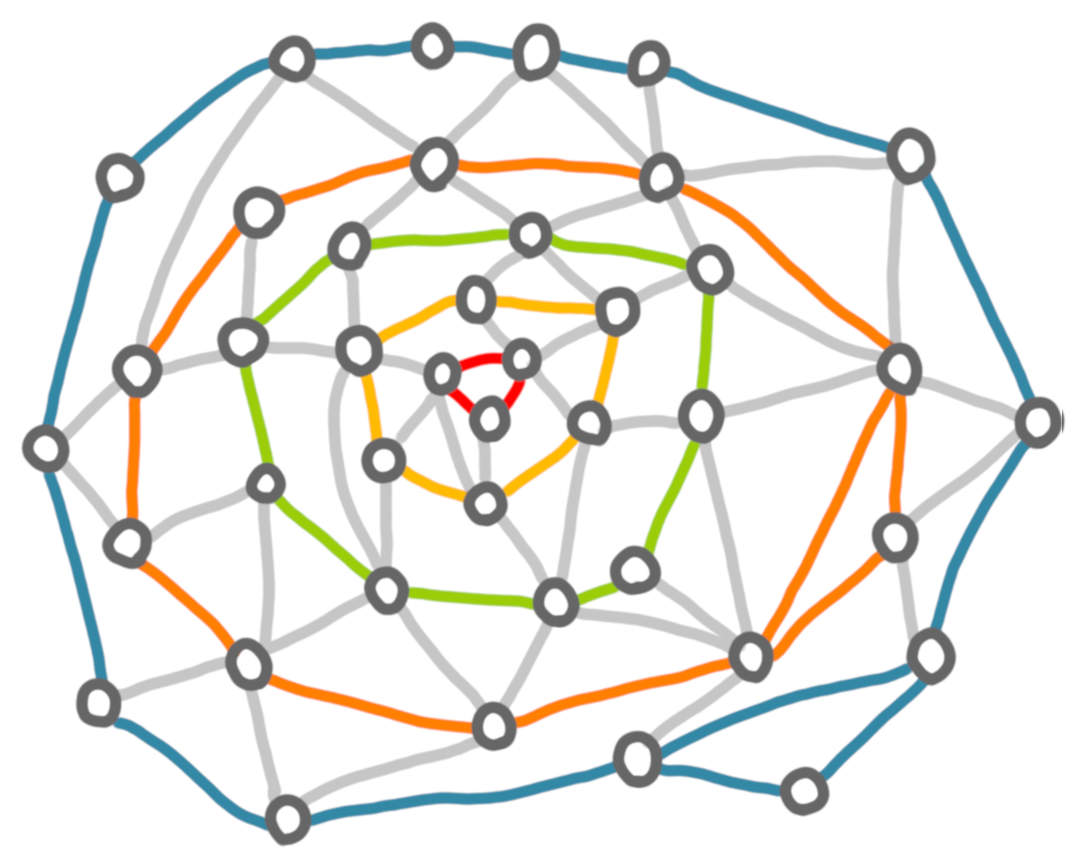
Now how to use this decomposition? The idea is that removing any layer divides the graph into two components: the part strictly outside the layer, and the part strictly inside. Then you can for example design approximation algorithms of the following form:

• remove a layer every $k$ layers, which creates a collection of groups of $(k-1)$ consecutive layers (here we put back the edge between these layers). For example if we remove the green layer we get:

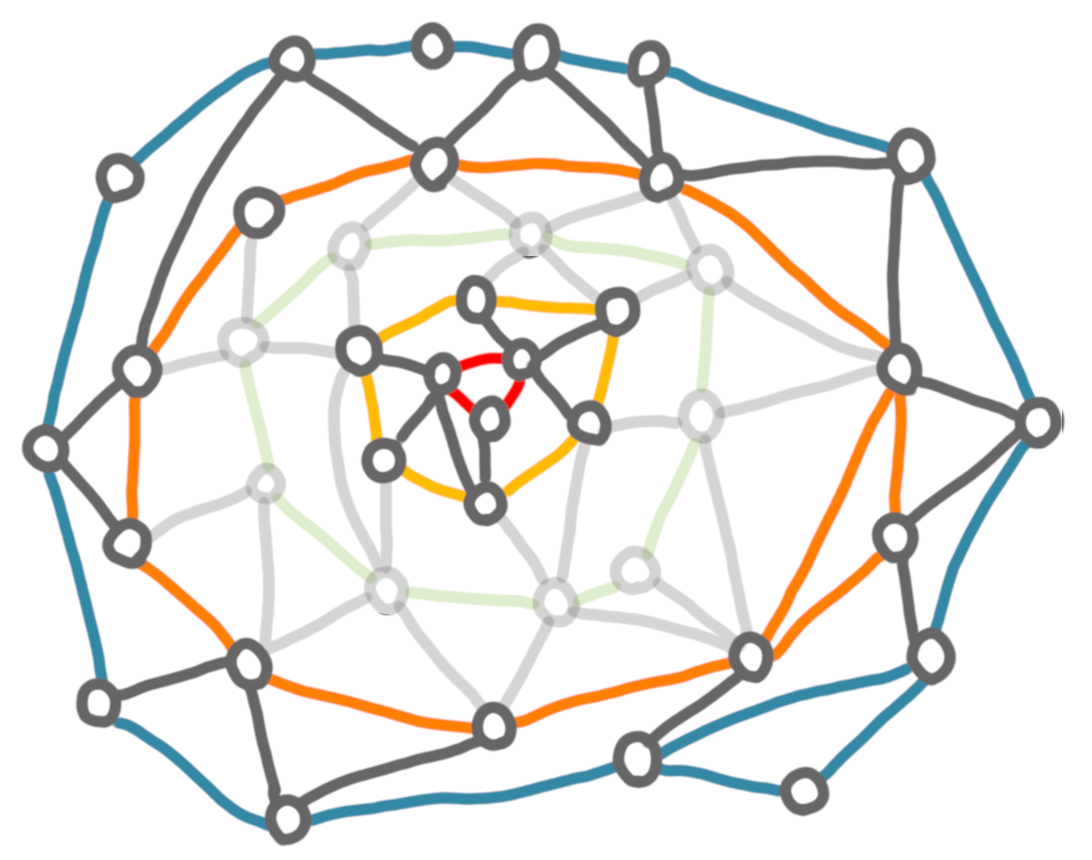
• solve optimally the problem on each groups of layers
• add back the removed layers, and fix some things if needed.

The idea is that if we are careful, we do not loose too much by forgetting about some layers, and solving the problem optimally on the groups of layers is not too hard because these have a constrained structure (small treewidth, k-outerplanar, etc.).

Graph burning

I saw a preprint on the arxiv about “graph burning”, and it made me curious. Graph burning is the following process. You have time steps, and at each time-step:

• you can choose an arbitrary vertex to burn
• a vertex that has burned before burns its neighbors.

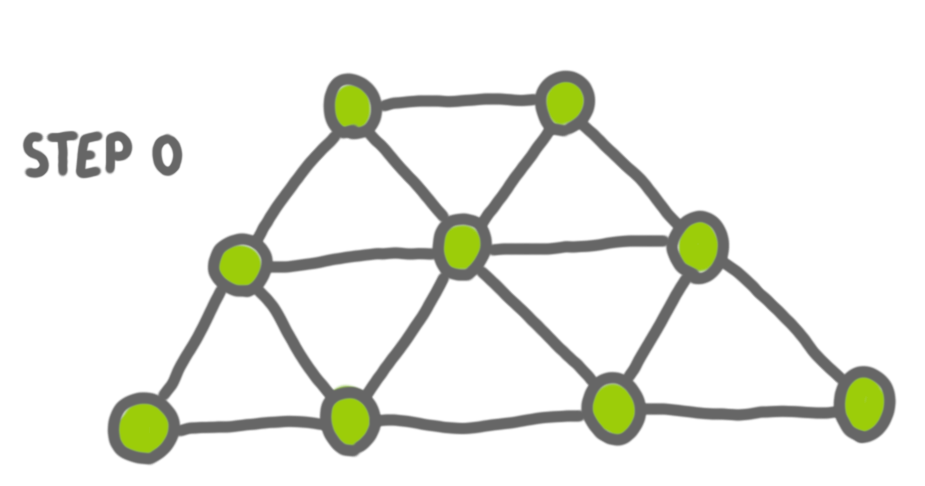
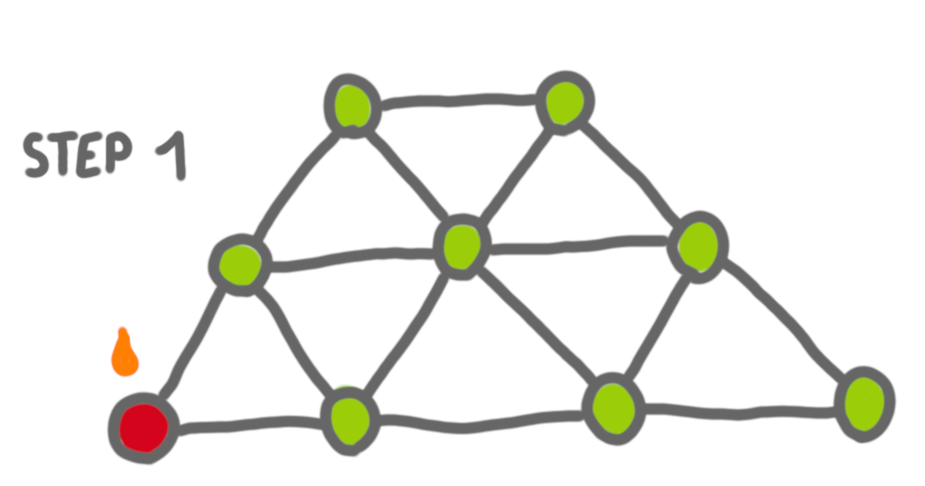
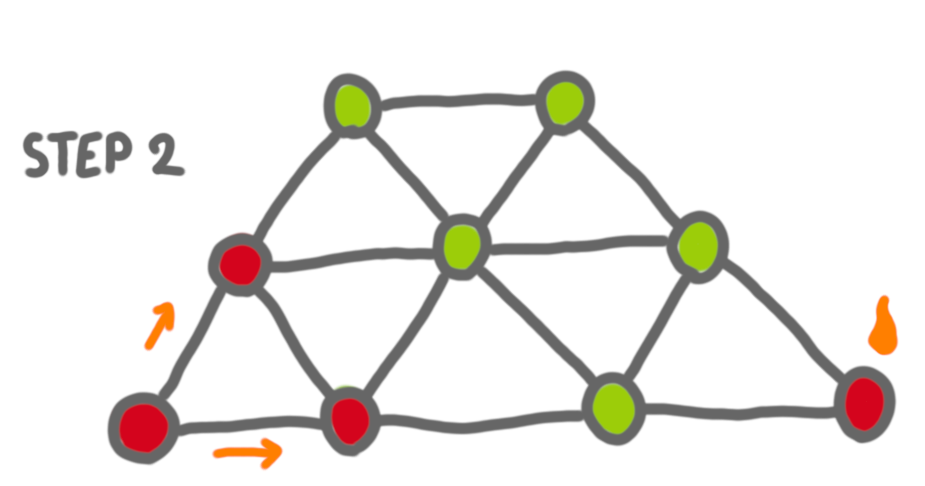
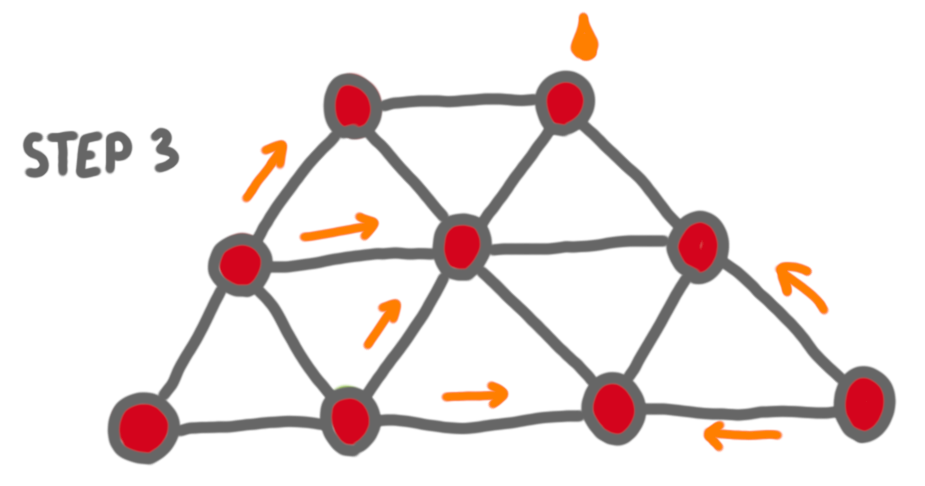
The burning number of a graph is the minimum number of steps before the whole graph is burned (this the optimal sequence of “external burns”).

A nice exercise is to prove that the burning number of an $n$-node path is (around) $\sqrt{n}$.