More November notes

18 Nov 2019

Some more notes for November 2019.

A picture from November 2019 in Chile.

Network creation game

Network generation models are mechanisms to create networks. In a classic setting the nodes arrive one after the other and are linked to nodes already in the network following some rules. In another setting, called network creation game the nodes are players, and they play a game in which they can choose to pay to be linked to other nodes. The outcome of the game is a network. The cost that a player pays is $\alpha$ for every node it decides to be linked to, plus the sum of the distances from this node to all the other nodes. In other words, a node wants to have short distance to every node, but cannot add a link to every node, because it would be too expensive.

For this game one can study the usual objects of algorithmic game theory: the Nash equilibrium and the price of anarchy.

It is conjectured that the price of anarchy is constant for any value $\alpha$, and this recent preprint makes progress on the conjecture.

Lempel-Ziv compression algorithms

Lempel-Ziv algorithm is a classic compression algorithm (or more precisely a classic family of algorithms, are there are several versions). A blog post on Semidoc describes the algorithm and gives an overview of this paper which studies how the compression rate can change when the original text is changed by one bit.

Two recent papers on arxiv deal with Lempel-Ziv:

The first one gives a new analysis of the fact that Lempel-Ziv is optimal for some models of random text (hidden Markov sources)
The second one improves the complexity of the algorithm decompressing the text.

Multi-armed bandit

Multi-armed bandit is an expression that appears here and there in TCS conference, and very often in theoretical machine learning. It is a type of problem where one has to make decisions one after the other, to maximize some pay-off. Basically, at each round, it has the choice between several options called the “arms” of the bandit (like the levers of different slot-machines).

A basic version is the following framework:

Given: $k$ arms, $T$ rounds.

In each round $t\in[T]$:

Algorithm picks arm $a_t$.
Algorithm observes reward $r_t\in [0,1]$ for the chosen arm.

Pay-off: the sum of the rewards

The reward for an arm comes from an unknown distribution, but if the algorithm chooses an arm repeatedly, it somehow learns this distribution. There is already a lot to say on this simple case, and there are a flurry of papers about this, these days.

Here is a recent introduction to multi-armed bandit. Also if you are in Rennes, France, on Wednesday there is a PhD defense on this topic.

Delaunay triangulations have perfect matchings

Delaunay triangulations are triangulations of point sets in the plane. I recentely learnt that the graphs that are Delaunay triangulations, always have a perfect matching (that is a matching of size $n/2$ if $n$ is even, and $(n-1)/2$ is $n$ is odd).

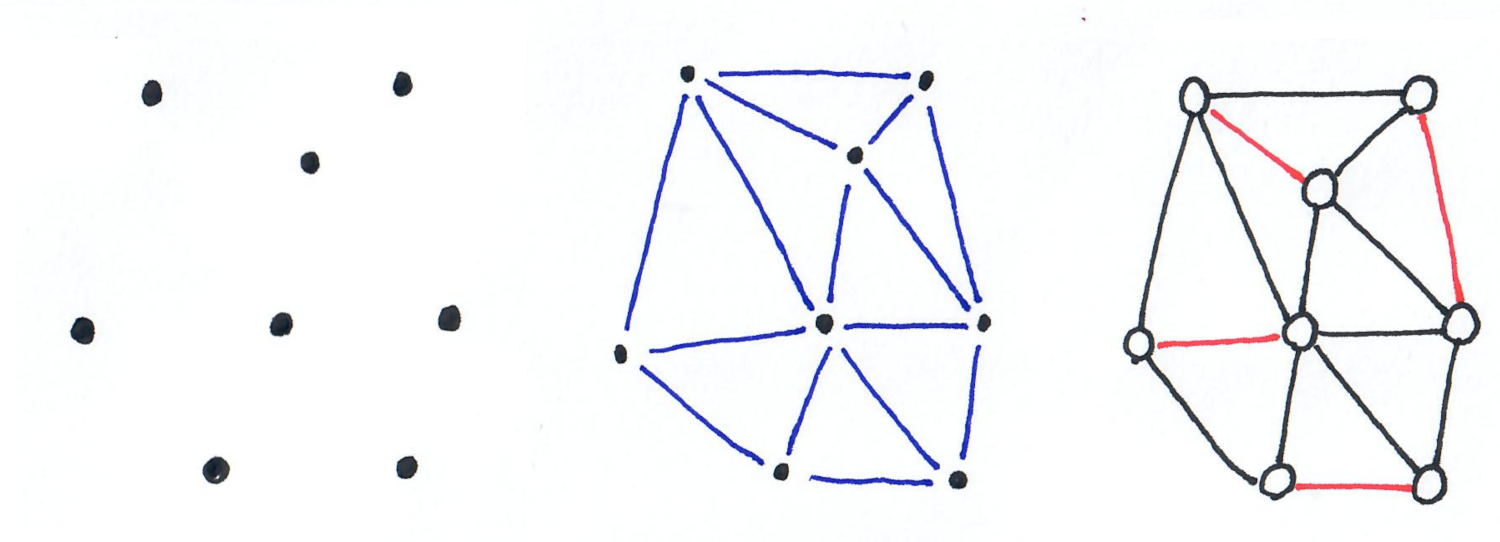
A point set, its Delaunay triangulation, and the associated graph with a perfect matching.

A short proof of this appeared on arxiv recently, here. (Actually it is a stronger result that is proved, about the so-called “toughness” of Delaunay triangulations.)

Learning-augmented algorithms

Learning-augmented algorithms are algorithms that can use informtation coming from some machine learning source. Here is an example.

Binary search takes $O(\log n)$ in the worst-case. Now if you have some neural network (NN) telling you that the element you’re looking for is around position $i$, how do you modify your search? Well you can begin by testing position $i$. Then, if the NN is not perfect, this might not be the right value, but maybe it’s close. Say the value you’re looking for is larger. Then you can try to find a position that has larger value than your element, for example by doing exponential guesses. Once you have both upper and lower bound, you can run the usual binary search.

If the error (that is, the number of positions between your element and the prediction of the NN) is $\mu$, then your algorithm runs in $O(\log \mu)$. This is good: if the prediction is good then you speed up the search, and if it’s bad, then you do not loose much.

In more general terms, one looks for two properties:

consistency: the better the prediction, the better the algorithm
robustness: if the predition is bad, then the algorithm does not get much worse.

Note that for real application, one might also be interested in the running time of the NN, and a lot of other things.

Some material on this topic:

Discrete notes About Archive