A distributed computing view of plants
26 Mar 2021I’ve recently been interested in understanding the structure of living beings using the algorithmic lens, and in particular the structure of plants. A classic model in this domain is the notion of L-system, a form of grammar. I’ll describe the L-systems in a later post, but today I’d like to just write the thoughts that come to mind when thinking about this topic with distributed computing tools in mind.
From trees to trees
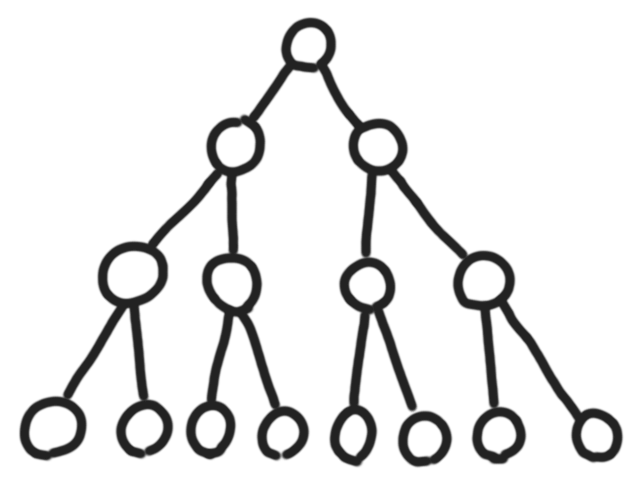
Trees in the CS/maths sense are quite different from real trees.
 |
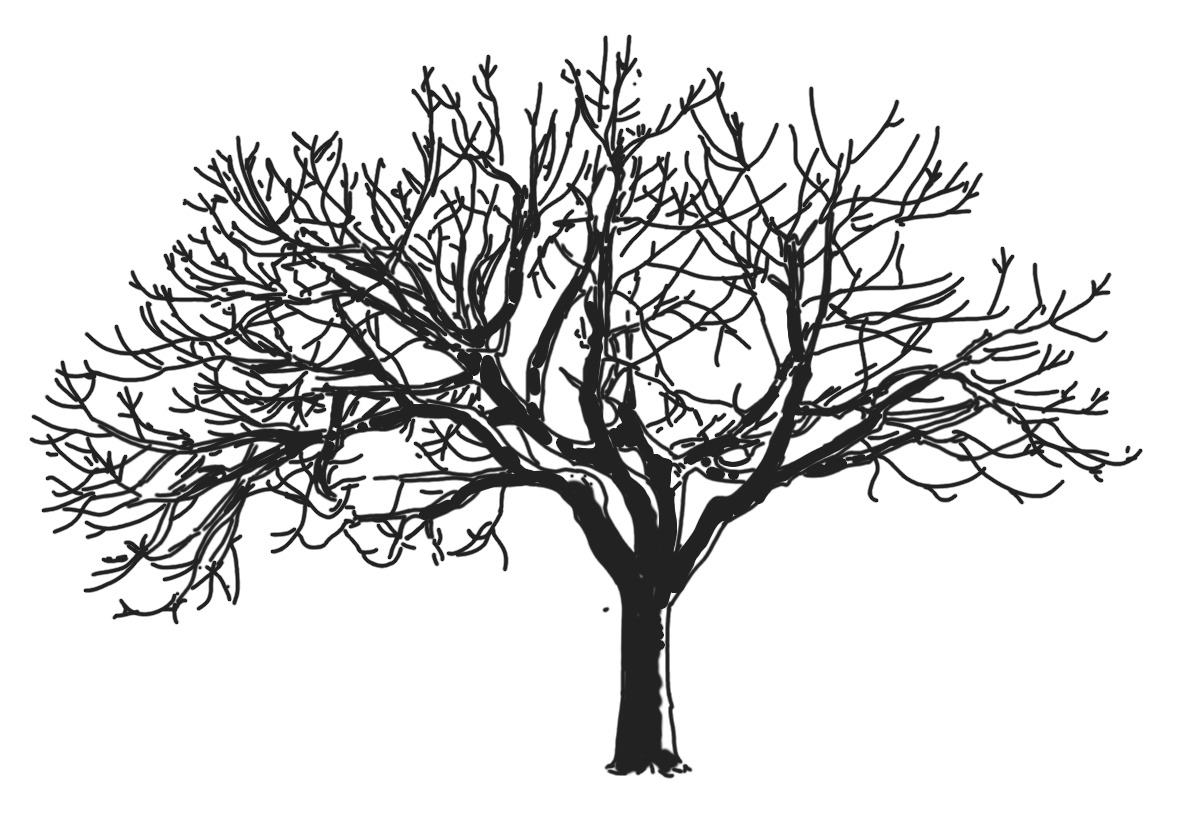 |
Even if we root both trees on the bottom, there are several step to take to transform a mathematical tree into some representation that looks like a real tree. Two mandatory steps are to add thickness and length to the edges, and to embed the graph in 3D. I guess the first step can be modeled by some system of weights on the edges, and the second would need at least some local encoding of angles between the edges.
But for now, let’s just think about graphs, and see what we can say.
A first model
Let’s try to think about how one would “generate a tree”. For someone with an algorithmic background the first idea is probably to consider a rule such as:
- start from a single node (the seed)
- apply recursively a local rule of the form “a leaf can be transformed into an internal node with two leafs”:

Apart from the topics of thickness and 3D, can we be satisfied with this model? Not quite. Let’s look at a few problems.
-
The models generates infinite trees. We have not mentioned any termination, so the result of our generative process is an infinite tree, and (at least last time I checked) most real trees were finite. We can maybe say that we stop the process at some point and see what the object looks like. This is not that bad, as anyway trees grow, so you can think that the process is infinite, but slower and slower, until the death of the tree.
-
The process is synchronous. At least on the picture, I have assumed that at each step the local rule is applied on every leaf. This is probably too much to ask, as there is no global clock in a tree. Therefore, from a distributed computing point of view, the process is asynchronous. One can expect that the asymmetry of real trees is partly due to this asynchrony. Note that actually in Nature there are some kind of clocks: the cycle of days and nights, the cycle of seasons etc.
-
All nodes have 2 children. When looking at the pictures, this regularity seems wrong. Pictures like this seem more natural:
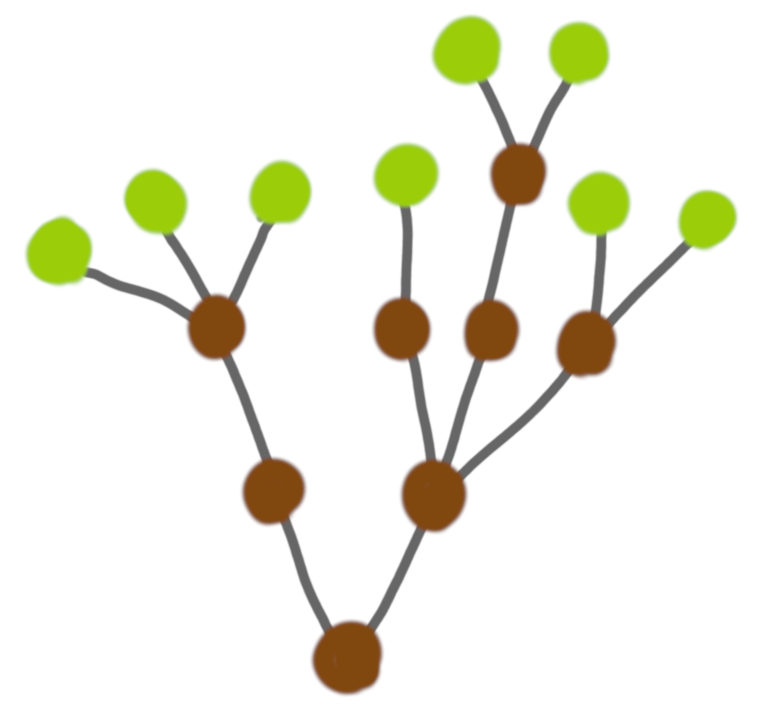
But on the other hand we said that the focus was on the mere graph structure, and then maybe a node with three leaves can be two binary nodes that would be very close once we add thickness and length. This seems to also make some sense from a biology point of view.

Anyway, let’s say that we do want to have a degree distribution that feels natural. (Note that we have not yet said how we want to evaluate the relevance of the models, so for now let’s say that we look for this undefined notion of “natural”).
Enriching the model
We do need to enrich the model with more than strictly local rules (except if we are fine with $k$-regular trees, for some $k$, but we are not). Then a natural idea is to think that all nodes hold some label (or letter if you are into automata, or color if you are into graph colorings). In terms of distributed computing, we can think of these labels/colors as constant size local memory. With this we can have more refined rules, such as:

Such enhanced rules create more interesting structures.
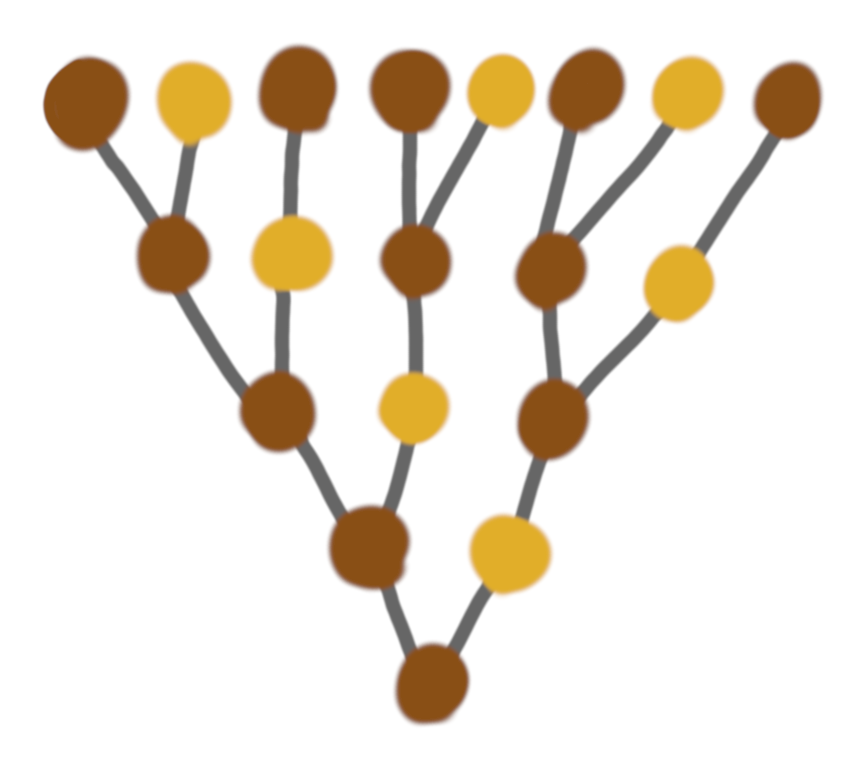
These structures are nicer, but still very rigid, and quite unnatural.
To avoid this effect one can add some probability to the model. On the one hand, it will add some variance to the shape, thus make it look more natural, and on the other hand it seems reasonable from a biology point of view to assume that not everything is deterministic.
Going further and questions
Is this satisfying? The structures created would indeed look more like plants. One issue is that the result is somehow fractal, or at least everywhere the same in the tree: a node with label $A$ will always generate the same probabilistic distribution of branches. This is probably fine for some plants which have very regular shapes. A well-known example of such a plant is the Romanesco broccoli.

But real trees are not so fractal-like. For example one can see that the lowest part is very different from the upper part. This implies that the generation process is not purely local.
There are two natural way to understand this. One way is to assume that these differences between different part of the tree come from the environment, and then the environment should somehow appear in the rules. Another way is to assume that there is some global process going on, for example some communication between the different parts of the tree. From a distributed computing perspective this could be captured by considering a memory at each node, with some more complicated dynamics. In this perspective, a lot of questions come to mind:
-
What is the size of this memory? For example, if we capture some plant structures by a class of (mathematical) trees, what is the minimum size of the local memory to generate this class? (This would be close to the approach that people have been successfully developing for understanding ants, see for example Amos Korman’s research.)
-
Is this memory mutable, that is can it change during the process, or is it non-mutable, that is, it is fixed once the node is created? (If it is fixed, then we basically have the same model as with the labels, but with non-constant size which allows for a lot more flexibility.)
-
What can we say about robustness? What if we want some type of structure, or some properties (eg many leaves) but there are faults, or some probabilistic behavior? Can we ensure some fault-tolerance?
Clearly this set of questions come to my mind because of my distributed computing background, and one would have to check what are the meaningful ones from a biology perspectives.
In a next post I will try to give an overview of the L-systems, and of their extensions, which are quite close to what I’ve described intuitively above, but with the vocabulary of formal grammars (which might not be the best angle to answer the quantitative questions above).