Quick read: Low crossing numbers
20 Jan 2023In December, I participated in an algorithms/OR mini-workshop, where I attended the talk of Mónika Csikós about her work on structures with low crossing number (more precisely: this paper and that paper with Nabil Mustafa). Here is a glimpse of it.
Set systems and crossing number
A set system $(X,S)$ is just a ground set $X$ with a family of subsets $S$. Alternatively, you can think of an hypergraph: a set of vertices with a set of hyperedges. I will use both points of view.
The picture below illustrates a set system with $S=${$S_1, S_2, S_3, S_4$}.
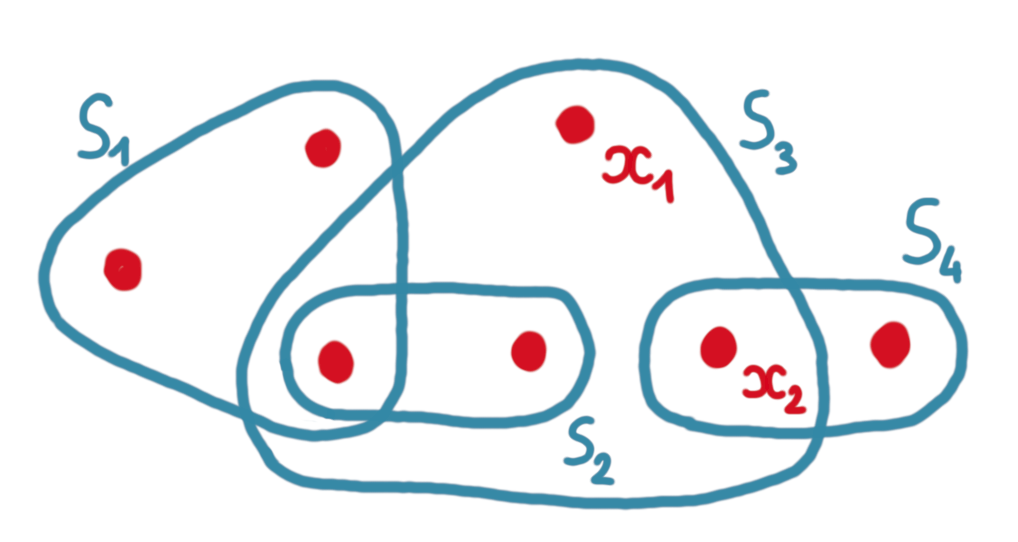
Now, consider a pair of vertices $x,y \in X$. Such a pair crosses an hyperedge if it has one endpoint in the hyperedge, and one endpoint out of it. For example in the picture above $(x_1,x_2)$ crosses $S_4$ (but no other hyperedge).
We are interested in computing a graph $G$ on top of the hypergraph, whose vertex set is equal to the vertex set $X$ of the hypergraph, and whose edge set $E\subseteq X^2$ is such that:
- it satisfies some structural constraints, for example being a spanning path or a spanning tree or a perfect matching ;
- it has low crossing number which means that for every hyperedge $S_i$, the number of edges of $G$ crossing $S_i$ is small.
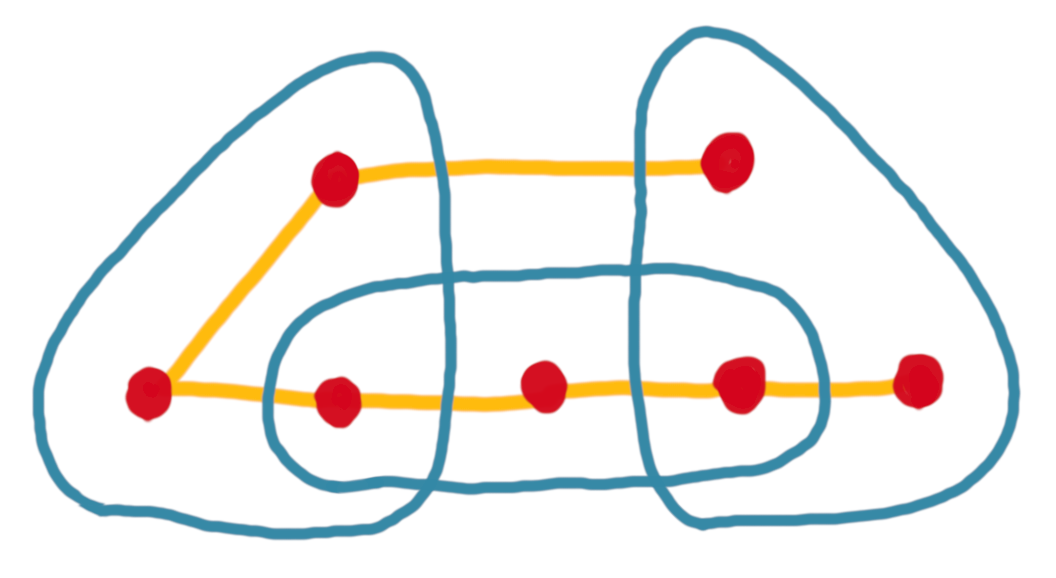
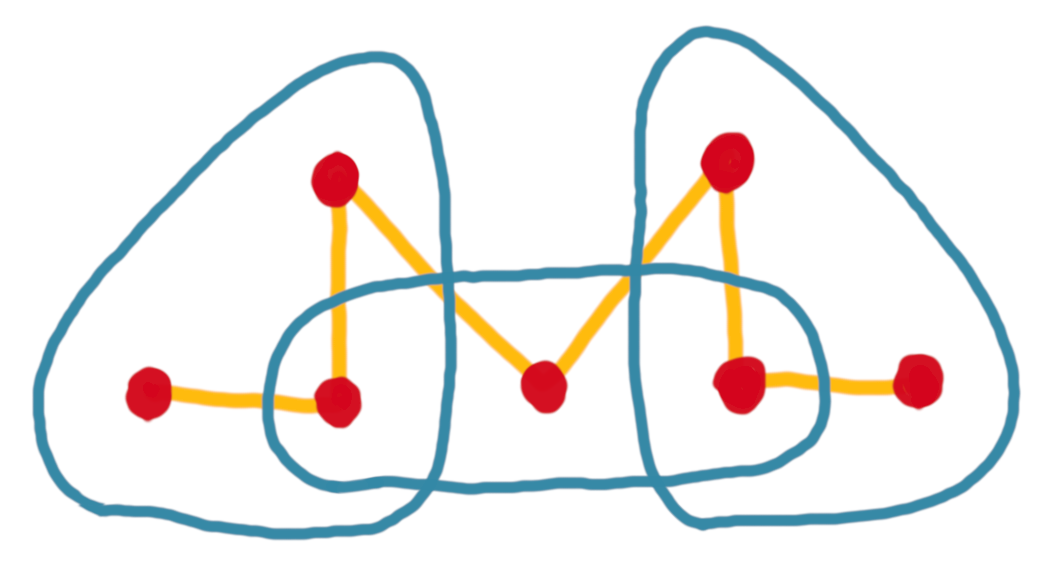
For example, below are two spanning paths for the same set system. The first one has crossing number 2 (every hyperedge is crossed at most twice), while the second has crossing number 6, because the hyperedge in the middle is crossed six times.
An application
Such structures with low crossing number have a lot of applications in geometry, theory of ML, and discrepancy theory. Here is a simple example.
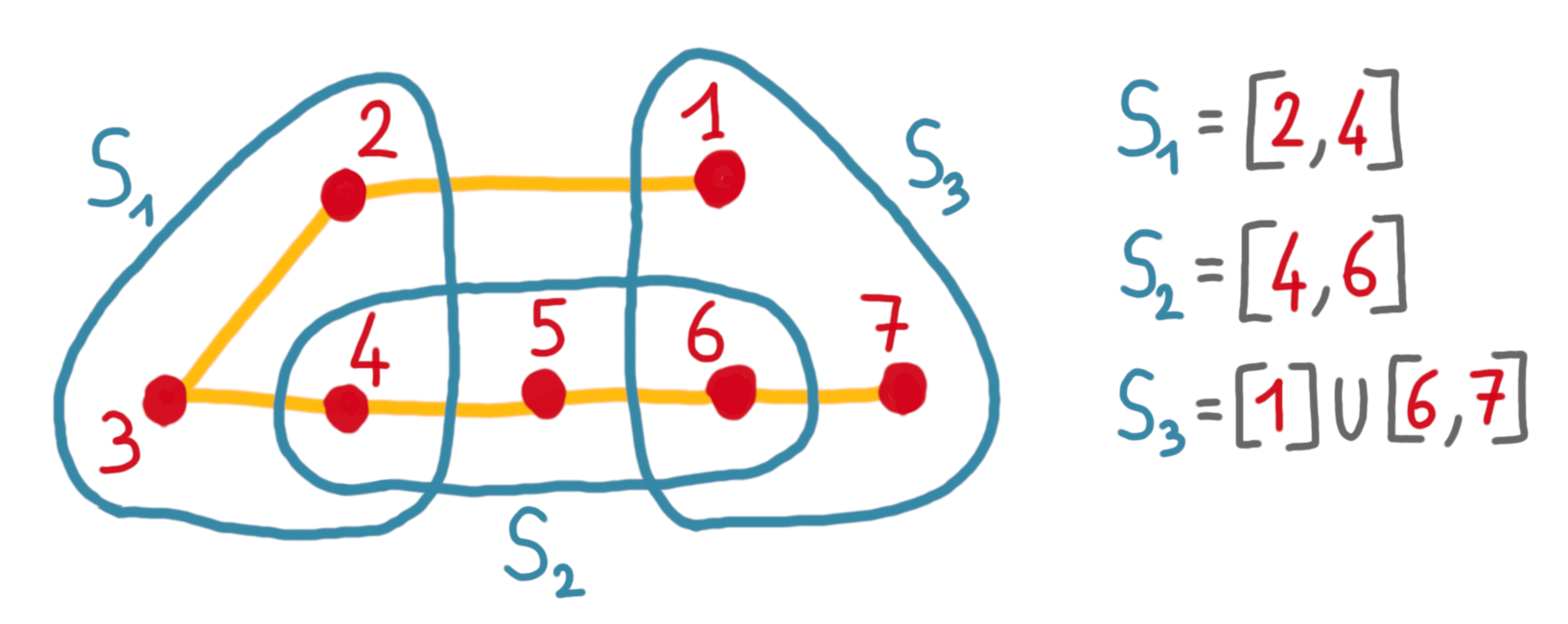
Suppose you have a huge set system, and you want a very compact data structure to answer queries of the form “list the points in hyperedge X”. If you have a spanning path with low crossing number, this is easy. Indeed, you just have to store the points in the order of the path, and then for every hyperedge store a few intervals. This is because for any hyperedge the path crosses the border only a small number of times, and it is enough to remember what are the points of entry and exit. See the picture below.
A condition for existence
To get some intuition about the crossing number, consider a hypergraph that contains all the possible hyperedges on a set of $n$ vertices. This hypergraph does not have a spanning path of crossing number lower than $n-1$. Indeed, for any path, the hyperedge that takes every other vertex of the path is crossed $n-1$ times. See the picture below.
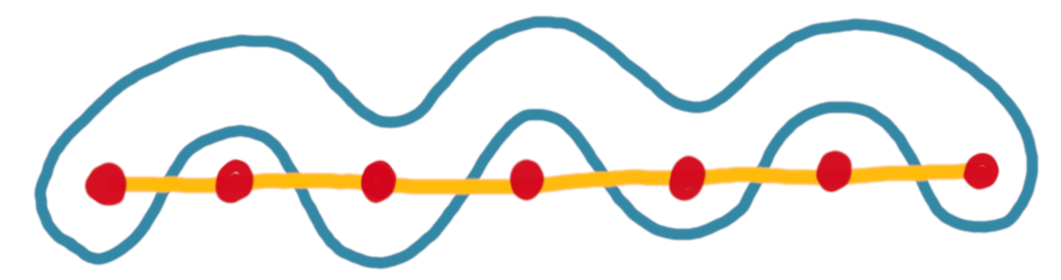
It is actually a challenge to get crossing number $o(n)$, and it is already useful to have this, hence when we say “low crossing number”, we mean “crossing number $o(n)$”. Note that the example above shows that we cannot always hope for a spanning path with a low crossing number. Nevertheless, by bounding some structural parameters of the hypergraph one can ensure that a spanning path with low crossing number exists. Specifically:
Theorem: If the dual VC dimension of $(X,S)$ is at most $d$, then there exists a spanning path with crossing number $O(n^{1-1/d})$.
I don’t want to define the dual VC dimension here, since it is not needed for the rest of the post, and it is a bit of a mouthful. But let’s just say that bounding it rules out the behavior above, while many natural hypergraphs do have a bounded dual VC dimension (including the ones arising from geometry, which is one of the main applications of what we discuss here).
The previous algorithm
In 1989, Chazelle and Welzl gave a polynomial algorithm for computing a spanning tree with low crossing number (see this paper) under the assumption of the theorem above. The main contribution of Csikós-Mustafa paper is to improve the complexity by modifying the algorithm in several clever ways. For the explanation we will keep the example of a spanning paths, but again it could be a spanning tree or a perfect matching.
The original algorithm follows the intuition of the multiplicative weight update method. The algorithm defines and updates a weight for every hyperedge and a cost for every edge (here edge simply means an element of $X^2$, or in other words, we have an underlying clique). The cost of an edge will simply be the sum of the weights of the hyperedges it crosses. Let’s see the pseudo-code and then comment on it.
- Initially, every hyperedge has weight 1.
- For $i=1$ to $n-1$:
- Select an edge $e$ with minimum cost, and add it to the path.
- Double the weight of any hyperedge that is crossed by $e$.
- Remove all vertices that have two incident edges selected (i.e. those that do not need more edges, since we look for a path).
Intuitively, here is what’s going on. Since, we want to minimize the maximum crossing number of an hyperedge, one wants to keep an eye on the hyperedges that are already crossed by a lot of selected edges, and try to avoid adding even more edges crossing them. In the algorithm, an hyperedge in this situation will have a high weight, hence in general the algorithm will not pick an edge that is crossing it. The magic of the multiplicative weight update method (and of the dual VC dimension) is that doubling the weights allows to get theoretical guarantees on the outcome.
Now the complexity of this algorithm is basically the cost of finding the edge of minimum cost for each iteration of the loop, which leads to $O(mn^3)$ (where $n$ is the size of $X$ and $m$ is the size of $S$).
Key new idea: sampling edges
The new algorithm achieves complexity of $\tilde{O}(mn^{1/d}+n^{2+1/d})$. The dependency in $d$ might seem counter-intuitive: the larger the parameter, the fastest they solve the problem. But remember that the goal is to compute a spanning path with crossing number $O(n^{1-1/d})$, hence the target becomes easier to reach when $d$ increases.
For the new algorithm, the key idea is to avoid the costly procedure of finding the edge with the smallest cost. Instead, we will do some sampling. That is, we define weights for edges, and sample according to these weights, which means that the probability of picking an edge will be proportional to the weight. Just to clarify the vocabulary: now both edges and hyperedges have weights, and there are no cost anymore.
So how do we update the weights of the edges in order to give more weights to the ones that do not cross already-heavy hyperedges? One way would be, for every edge, to go over the hyperedges it crosses and infer some weight, but we would revived the $O(mn^2)$ we want to avoid. Instead the edge weight update will itself depend on a sampling.
Here is the pseudo-code of the modified algorithm.
- Initially, every hyperedge and every edge has weight 1.
- For $i=1$ to $n-1$:
- Sample an edge $e$ according to edge weights, and add it to the path.
- Sample a hyperedge $h$ according to hyperedge weights.
- Double the weight of any hyperedge that is crossed by $e$.
- Halve the weights of any edge that is crossing $h$.
- Remove all vertices that have two incident edges already in the path.
Thanks to sampling, the complexity of each loop is reduced. What is less clear is whether this is good enough to lead to a good path. And the answer is no a priori.
More new ideas
Something that makes the algorithm above deviate from the desired behavior is the innocent-looking last step of every loop (that is, removing the vertices that are useless) that messes up the structure of the weights. And the error is amplified, iteration after iteration. What the authors do is to reinitialize the weights periodically (a logarithmic number of times), to avoid too much deviation.
Finally, to gain even more on the complexity, they also do not fully perform the weight doubling and weight halving, and again sample (uniformly this time) for this step.
A very nice algorithm! And also an implementable one: the authors have an open-access code that can handle large instances.